【2021東京大学・文系】
\(a\) を正の実数とする.座標平面上の曲線 \(C\) を \(y=ax^3-2x\) で定める.原点を中心とする半径 \(1\) の円と \(C\) の共有点の個数が \(6\) 個であるような \(a\) のん範囲を求めよ.
考え方・解答・解説
\(y=ax^3-2x\) ・・・①
原点を中心とする半径 \(1\) の円: \(x^2+y^2=1\) ・・・②
①,②より
\(x^2+(ax^3-2x)^2=1\) より
\(a^2x^6-4ax^4+5x^2-1=0\) ・・・③
題意は,③の実数解が \(6\) 個になればよい.

\(t=x^2\) と置き換えることで,\(3\) 次方程式に変形することができます!
考え方や例題は、「置き換えによる2次関数の最大・最小[4STEP 162番]頻出重要問題・複二次式」を参考に!
ここで,\(t=x^2\) とおくと③は
\(a^2t^3-4at^2+5t-1=0\) ・・・④
このとき,\(t=0\) のとき④の解ではないので \(t>0\)
\(t>0\) を満たす任意の \(1\) つの \(t\) に対して,\(x\) は実数解を \(2\) つもつことになるため
題意を満たすためには,④を満たす正の実数 \(t\) が全部で \(3\) 個存在すればよい.

\(3\) 次方程式が解を \(3\) 個もつときの考え方は,定数分離できるかどうかで方針が変わりましたね!
本問では定数分離ができないため,「【2019早稲田大学・教育】非定数分離型・異なる3つの実数解を持つ条件」で学習した考え方を利用しましょう!
④の左辺を \(f(t)\) とおくと
\(f^{\prime}(t)=3a^2t^2-8at+5=(at-1)(3at-5)\)
\(f^{\prime}(t)=0\) のとき,\(t=\displaystyle\frac{1}{a}\) , \(\displaystyle\frac{5}{3a}\)
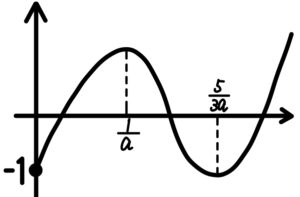
\(a>0\) より\(0<\displaystyle\frac{1}{a}<\displaystyle\frac{5}{3a}\) であるから,\(t>0\) における増減表は以下のようになる.
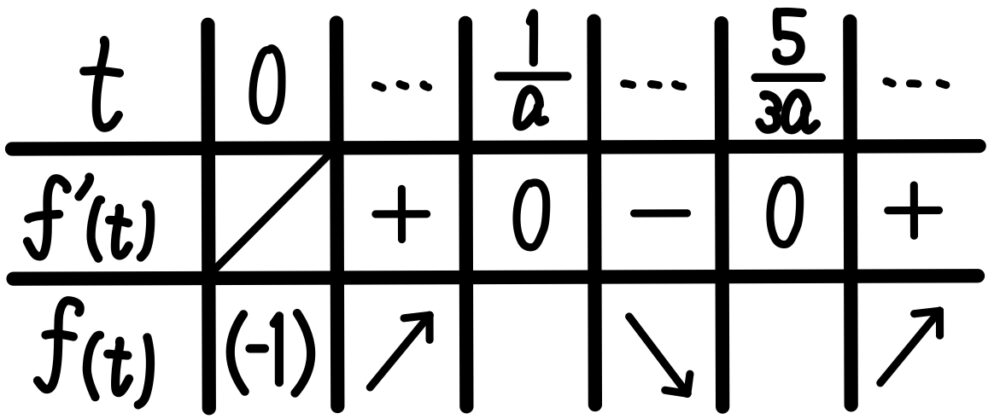
 ゆえに題意を満たすためには,
ゆえに題意を満たすためには,
\(f\left(\displaystyle\frac{1}{a}\right)>0\) かつ \(f\left(\displaystyle\frac{5}{3a}\right)<0\) を満たせばよい.
\(f\left(\displaystyle\frac{1}{a}\right)=\displaystyle\frac{2}{a}-1>0\) より \(0<a<2\)
\(f\left(\displaystyle\frac{5}{3a}\right)=\displaystyle\frac{50}{27a}-1<0\) より \(a>\displaystyle\frac{50}{27}\)
したがって,\(\displaystyle\frac{50}{27}<a<2\)








コメント