【2023福岡大学・医学部】三角関数のグラフ、極値、変曲点、面積

解答・解説

( ⅰ )

\(f(x)=4\tan^3x-9\tan^2x\) より

\(f^{\prime}(x)=(12\tan^2x-18\tan x)\cdot\displaystyle\frac{1}{\cos^2x}\)

\(=(12\tan^2x-18\tan x)(1+\tan^2x)\)

\(=12\tan^4x-18\tan^3x+12\tan^2x-18\tan x\)

\(f^{\prime}(x)=0\) のとき

\(f^{\prime}(x)=6\tan x(2\tan x-3)(1+\tan^2x)=0\)

\(\tan x=0,\displaystyle\frac{3}{2}\)

\(-\displaystyle\frac{\pi}{2}<x<\displaystyle\frac{\pi}{2}\) のとき

\(x=0,\alpha\) (ただし \(\alpha\) は，\(\tan \alpha=\displaystyle\frac{3}{2}\) かつ \(\displaystyle\frac{\pi}{4}<\alpha<\displaystyle\frac{\pi}{3}\) を満たす)

また，

\(f^{\prime\prime}(x)=\left(48\tan^3x-54\tan^2x+24\tan x-18\right)\cdot\displaystyle\frac{1}{\cos^2x}\)

\(=6(\tan x-1)(8\tan^2x-\tan x+3)(1+\tan^2x)\)

\(f^{\prime\prime}(x)=0\) のとき

\(\tan x=1\)

\(-\displaystyle\frac{\pi}{2}<x<\displaystyle\frac{\pi}{2}\) より

\(x=\displaystyle\frac{\pi}{4}\)

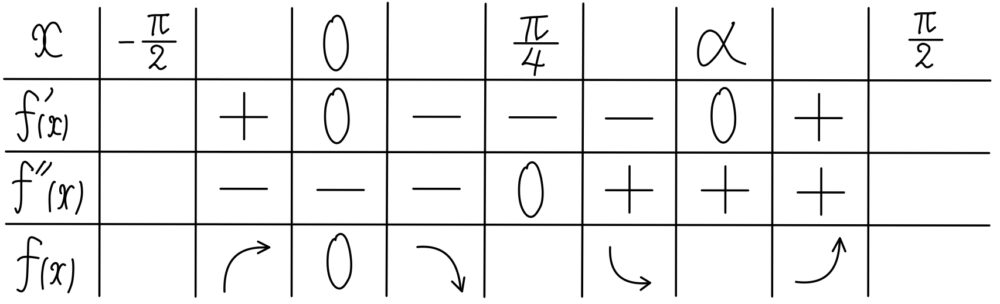
増減表から，\(x=0\) で極大，\(x=\displaystyle\frac{\pi}{4}\) で変曲点となる．

したがって， \(a=0\) , \(b=\displaystyle\frac{\pi}{4}\)

( ⅱ )

( ⅰ ) より与えられた不等式が表す領域は，下図の斜線部分．

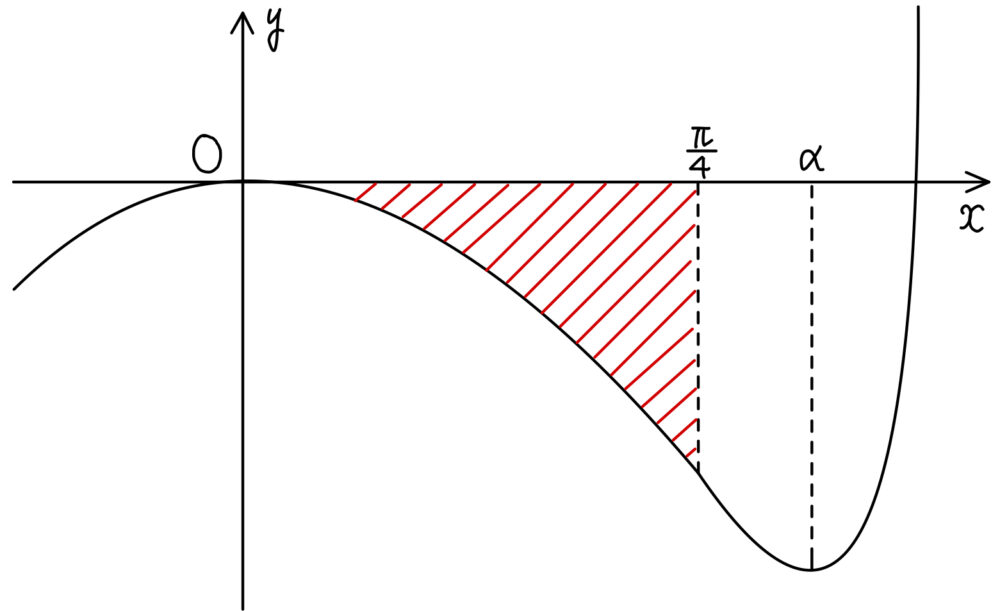
求める面積を \(S\) とすると

\(S=\displaystyle\int^{\frac{\pi}{4}}_{0} (4\tan^3x-9\tan^2x)dx\) ・・・①

ここで，

\(\displaystyle\int^{\frac{\pi}{4}}_{0} \tan^3x dx\)

\(=\displaystyle\int^{\frac{\pi}{4}}_{0} \tan x\left(\displaystyle\frac{1}{\cos^2x}-1\right) dx\)

\(=\displaystyle\int^{\frac{\pi}{4}}_{0}\left(\tan x\cdot\displaystyle\frac{1}{\cos^2x}-\tan x\right)dx\)

\(=\Bigl[\displaystyle\frac{1}{2}\tan^2x+\log{|\cos x|}\Bigr]^{\frac{\pi}{4}}_{0}\)

\(=\displaystyle\frac{1}{2}-\displaystyle\frac{1}{2}\log{2}\)

また

\(\displaystyle\int^{\frac{\pi}{4}}_{0} \tan^2x dx\)

\(=\displaystyle\int^{\frac{\pi}{4}}_{0} \left(\displaystyle\frac{1}{\cos^2x}-1\right) dx\)

\(=\Bigl[\tan x-x\Bigr]^{\frac{\pi}{4}}_{0}\)

\(=1-\displaystyle\frac{\pi}{4}\)

したがって，

\(S=-4\left(\displaystyle\frac{1}{2}-\displaystyle\frac{1}{2}\log{2}\right)+9\left(1-\displaystyle\frac{\pi}{4}\right)\)

\(=7+2\log{2}-\displaystyle\frac{9\pi}{4}\)