【2021数学ⅡB(第2日程)】第1問[2](三角関数)
(1)考察1:問題と解答・解説《シ〜タ》

(1)考察1:解答・解説《シ〜タ》
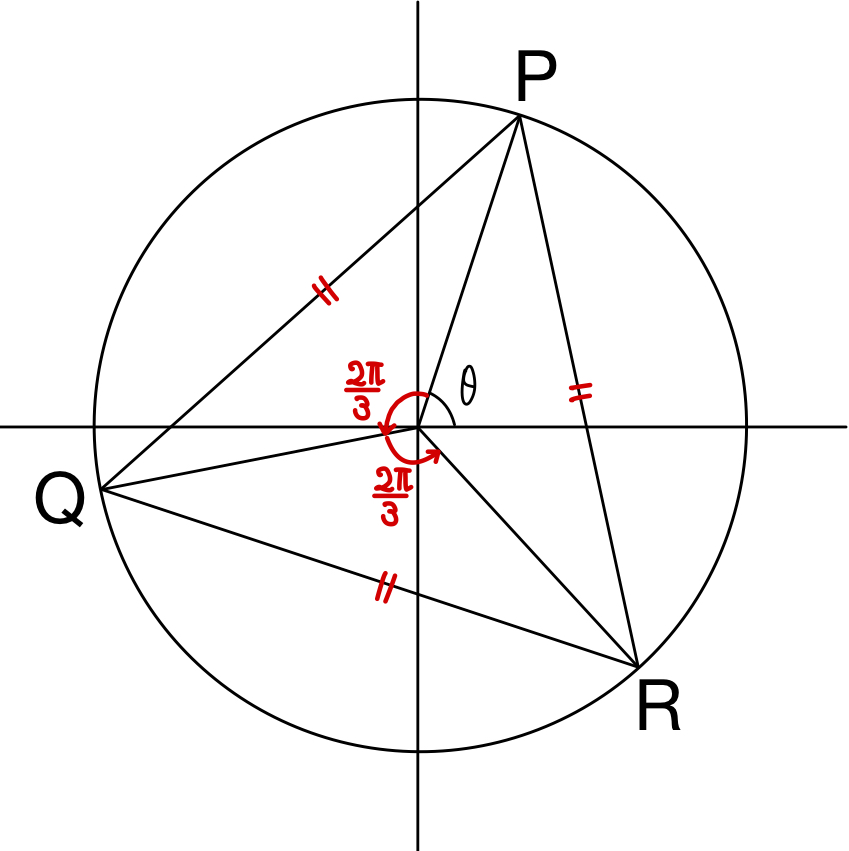
\(\triangle PQR\) が正三角形のとき
\(\alpha=\theta+\displaystyle\frac{2}{3}\pi\) ・・・《シ》
\(\beta=\theta+\displaystyle\frac{4}{3}\pi\) ・・・《ス》
加法定理より
\(\cos \alpha=\cos \left(\theta+\displaystyle\frac{2}{3}\pi\right)=\cos \theta\cos \displaystyle\frac{2}{3}\pi-\sin \theta\sin \displaystyle\frac{2}{3}\pi\) より
\(\cos\alpha=-\displaystyle\frac{\sqrt{3}}{2}\sin \theta-\displaystyle\frac{1}{2}\cos \theta\) ・・・《セ:⑦》
\(\sin \alpha=\sin \left(\theta+\displaystyle\frac{2}{3}\pi\right)=\sin \theta\cos \displaystyle\frac{2}{3}\pi+\cos \theta\sin \displaystyle\frac{2}{3}\pi\) より
\(\sin\alpha=-\displaystyle\frac{1}{2}\sin \theta+\displaystyle\frac{\sqrt{3}}{2}\cos \theta\) ・・・《ソ:④》
同様に,
\(\cos \beta=\cos \left(\theta+\displaystyle\frac{4}{3}\pi\right)=\cos \theta\cos \displaystyle\frac{4}{3}\pi-\sin \theta\sin \displaystyle\frac{4}{3}\pi\) より
\(\cos\beta=\displaystyle\frac{\sqrt{3}}{2}\sin \theta-\displaystyle\frac{1}{2}\cos \theta\)
\(\sin\beta=\sin \left(\theta+\displaystyle\frac{4}{3}\pi\right)=\sin \theta\cos \displaystyle\frac{4}{3}\pi+\cos \theta\sin \displaystyle\frac{4}{3}\pi\) より
\(\sin\beta=-\displaystyle\frac{1}{2}\sin \theta-\displaystyle\frac{\sqrt{3}}{2}\cos \theta\)
よって,
\(s=\cos \theta+\cos\alpha+\cos\beta\)
\(=\cos \theta+\left(-\displaystyle\frac{\sqrt{3}}{2}\sin \theta-\displaystyle\frac{1}{2}\cos \theta\right)+\left(\displaystyle\frac{\sqrt{3}}{2}\sin \theta-\displaystyle\frac{1}{2}\cos \theta\right)=0\)
\(t=\sin \theta+\sin\alpha+\sin\beta\)
\(=\sin \theta+\left(-\displaystyle\frac{1}{2}\sin \theta+\displaystyle\frac{\sqrt{3}}{2}\cos \theta\right)+\left(-\displaystyle\frac{1}{2}\sin \theta-\displaystyle\frac{\sqrt{3}}{2}\cos \theta\right)=0\)
よって,\(s=t=0\) ・・・《タ》
(1)考察2:問題と解答・解説《チ〜ネ》
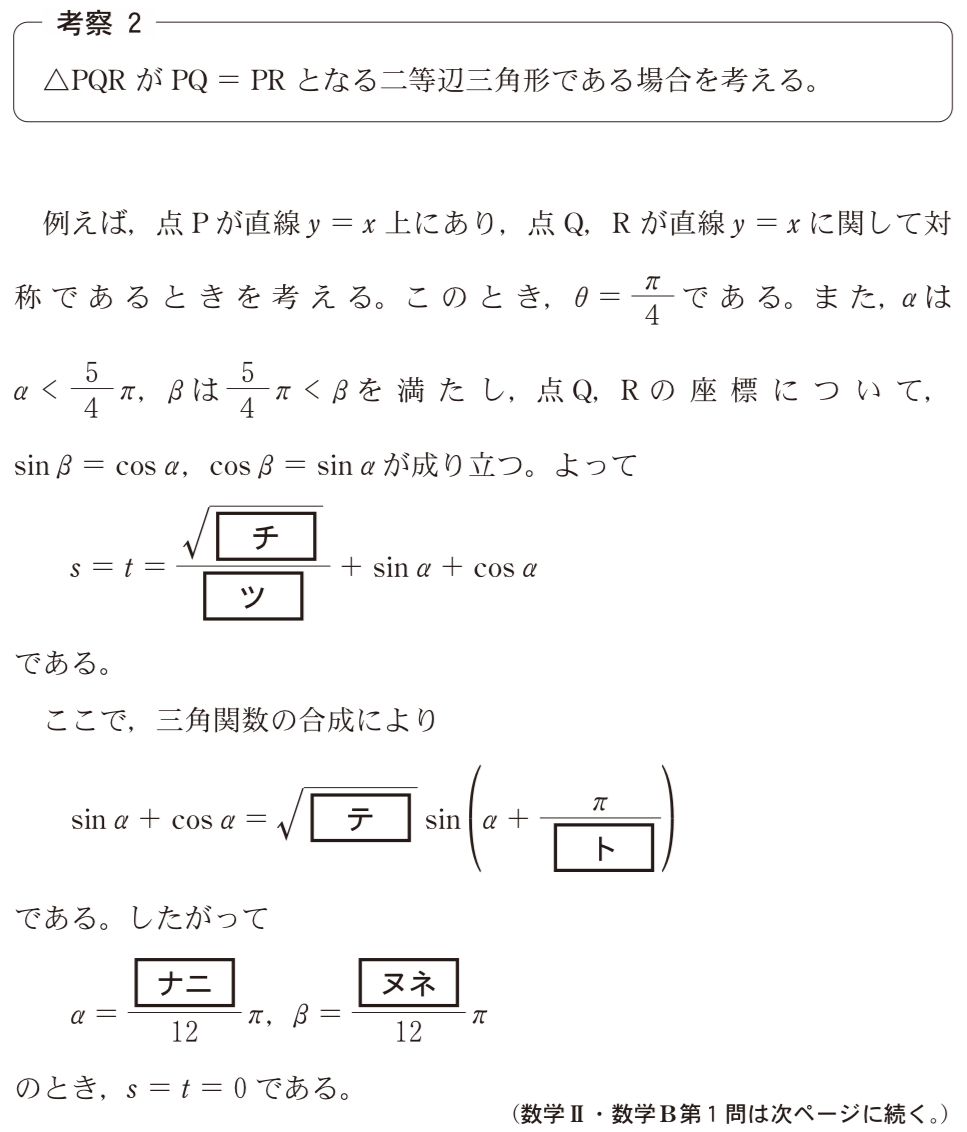
(1)考察2:解答・解説《チ〜ネ》
\(P\left(\cos\displaystyle\frac{\pi}{4},\sin\displaystyle\frac{\pi}{4}\right)=\left(\displaystyle\frac{\sqrt{2}}{2},\displaystyle\frac{\sqrt{2}}{2}\right)\) ,
\(Q(\cos\alpha,\sin\alpha)\) ,\(R(\cos\beta,\sin\beta)=(\sin\alpha,\cos\alpha)\) より
\(s=t=\displaystyle\frac{\sqrt{2}}{2}+\sin\alpha+\cos\alpha\) ・・・《チツ》
三角関数の合成から
\(\sin\alpha+\cos\alpha=\sqrt{2}\sin\left(\alpha+\displaystyle\frac{\pi}{4}\right)\) ・・・《テト》
\(s=t=0\) のとき
\(\sqrt{2}\sin\left(\alpha+\displaystyle\frac{\pi}{4}\right)+\displaystyle\frac{\sqrt{2}}{2}=0\)
\(\sin\left(\alpha+\displaystyle\frac{\pi}{4}\right)=-\displaystyle\frac{1}{2}\)
\(\displaystyle\frac{\pi}{4}<\alpha<\displaystyle\frac{5}{4}\pi\) より
\(\displaystyle\frac{\pi}{2}<\alpha+\displaystyle\frac{\pi}{4}<\displaystyle\frac{3}{2}\pi\) であるから
\(\alpha+\displaystyle\frac{\pi}{4}=\displaystyle\frac{7}{6}\pi\)
よって,\(\alpha=\displaystyle\frac{11}{12}\pi\) ・・・《ナニ》
\(\displaystyle\frac{\alpha+\beta}{2}=\displaystyle\frac{5}{4}\pi\) より
\(\beta=\displaystyle\frac{5}{2}\pi-\alpha=\displaystyle\frac{5}{2}\pi-\displaystyle\frac{11}{12}\pi\)
\(\beta=\displaystyle\frac{19}{12}\pi\) ・・・《ヌネ》
(2)考察3:問題と解答・解説《ノ〜ヘ》

(2)考察3:解答・解説《ノ〜ヘ》
\(s=0\) \(\iff\) \(\cos \theta+\cos\alpha+\cos\beta=0\)
よって \(\cos \theta=-\cos\alpha-\cos\beta\)
\(t=0\) \(\iff\) \(\sin \theta+\sin\alpha+\sin\beta=0\)
よって \(\sin\theta=-\sin\alpha-\sin\beta\)
\(\sin^2\theta+\cos^2\theta=1\) より
\((-\sin\alpha-\sin\beta)^2+(-\cos\alpha-\cos\beta)^2=1\)
\(2+2(\cos\alpha\cos\beta+\sin\alpha\sin\beta)=1\)
よって,\(\cos\alpha\cos\beta+\sin\alpha\sin\beta=\displaystyle\frac{-1}{2}\) ・・・《ノ〜ヒ》
\(\cos\left(\beta-\alpha\right)=\displaystyle\frac{-1}{2}\)
また同様に,
\(\cos \theta\cos\alpha+\sin\theta\sin\alpha=\displaystyle\frac{-1}{2}\)
\(\cos\left(\alpha-\theta\right)=\displaystyle\frac{-1}{2}\) であるから
\(0≦\theta<\alpha<\beta<2\pi\) に注意すると
\(\beta-\alpha=\alpha-\theta=\displaystyle\frac{2}{3}\pi\) ・・・《フヘ》
(3)問題と解答・解説《ホ》

(3)解答・解説《ホ》
考察1より「\(\triangle PQR\) が正三角形 ならば \(s=t=0\)」
考察3より「\(s=t=0\) ならば \(\triangle PQR\) が正三角形」であるから,《ホ:⓪》








コメント