【2021数学ⅠA(第1日程)】第2問[2](データの分析)

(1)問題と解答・解説《タ〜チ》
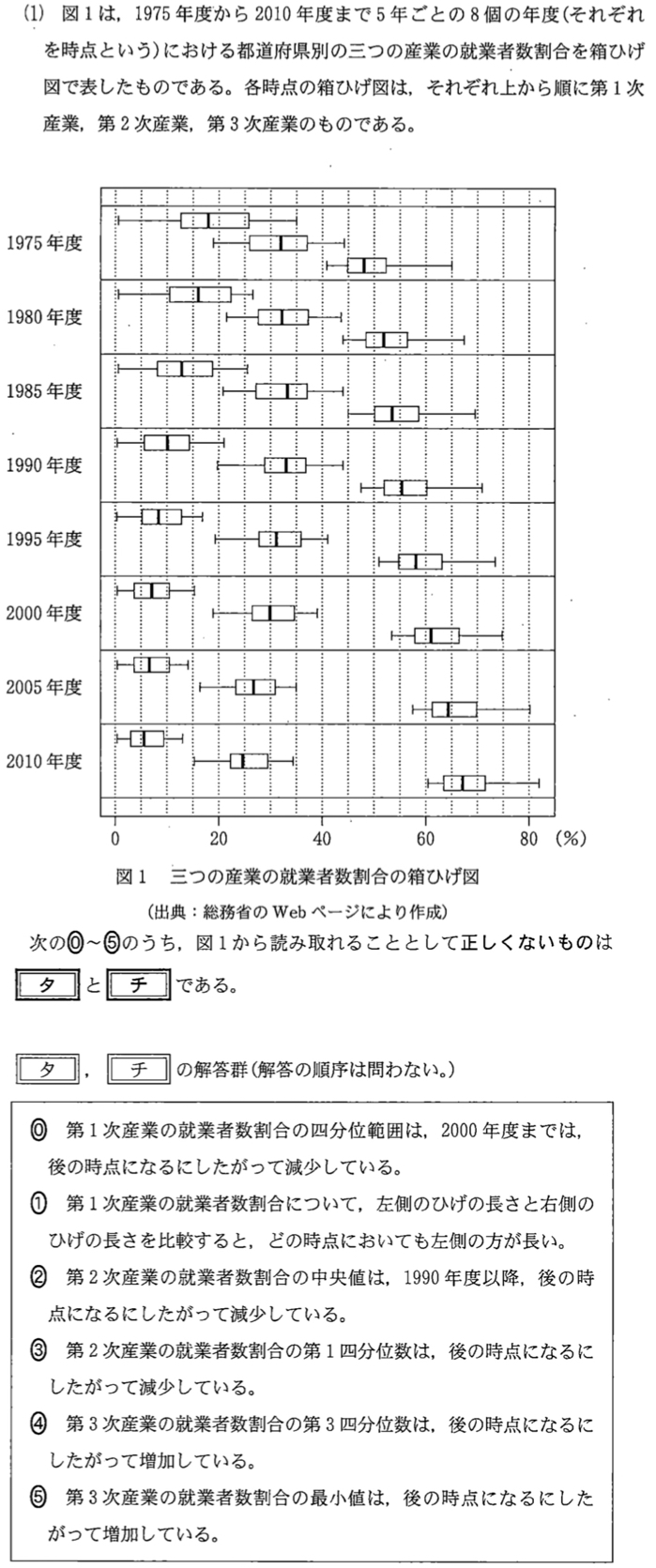
(1)解答・解説《タ〜チ》
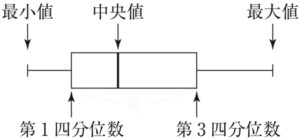

四分位範囲とは,箱ひげ図における第3四分位数と第1四分位数の差のことですね!
⓪について
\(1975\) 年度から \(2000\) 年度まで四分位範囲は減少しているため,正しい.
①について
\(1990\) 年度,\(2000\) 年度,\(2010\) 年度については,右側のひげの長さが左側のひげの長さより長いため,正しくない.
②について
\(1990\) 年度以降,第 \(2\) 次産業の就業者割合の中央値は減少しているため,正しい.
③について
第 \(2\) 次産業の就業者割合の第 \(1\) 四分位数は,\(1975\) 年度から \(1980\) 年度,\(1985\) 年度から \(1990\) 年度に増えているため,正しくない.
④について
第 \(3\) 次産業の就業者割合の第 \(3\) 四分位数は,後の時点になるにしたがって増加しているため,正しい.
⑤について
第 \(3\) 次産業の就業者割合の最小値は,後の時点になるにしたがって増加しているため,正しい.
したがって,正しくなくものは①と③ ・・・《タチ》
(2)問題と解答・解説《ツ〜テ》
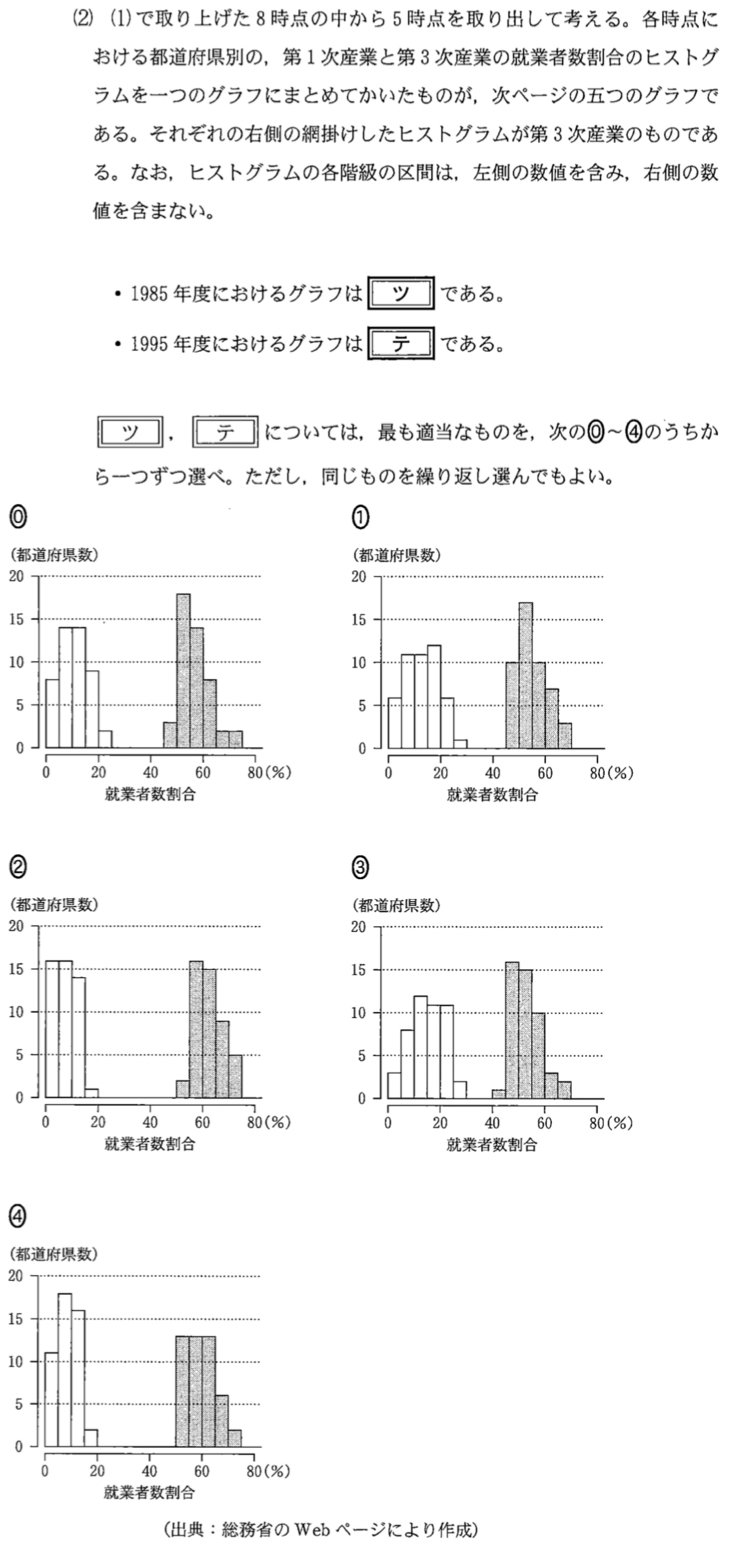
(2)解答・解説《ツ〜テ》
\(1985\) 年度の第 \(1\) 次産業の就業者割合の最大値は(1)の箱ひげ図から,\(25\) %以上 \(30\) %未満であるから,条件を満たすヒストグラムは①または③
また,\(1985\) 年度の第 \(3\) 次産業の就業者割合の最小値が \(45\) %であることに注目すると,\(1985\) 年度のヒストグラムは① ・・・《ツ》
次に,\(1995\) 年度の第 \(1\) 次産業の就業者割合の最大値は(1)の箱ひげ図から,\(15\) %以上 \(20\) %未満であるから,条件を満たすヒストグラムは②または④
また,第 \(3\) 次産業の就業者割合の中央値は,\(47\) 都道府県において小さい方から \(24\) 番目だが,ヒストグラムより,②の中央値は \(60\) %以上 \(65\) %未満,④の中央値は \(55\) %以上 \(60\) %未満であるから,\(1995\) 年度のヒストグラムは④ ・・・《テ》
(3)問題と解答・解説《ト》
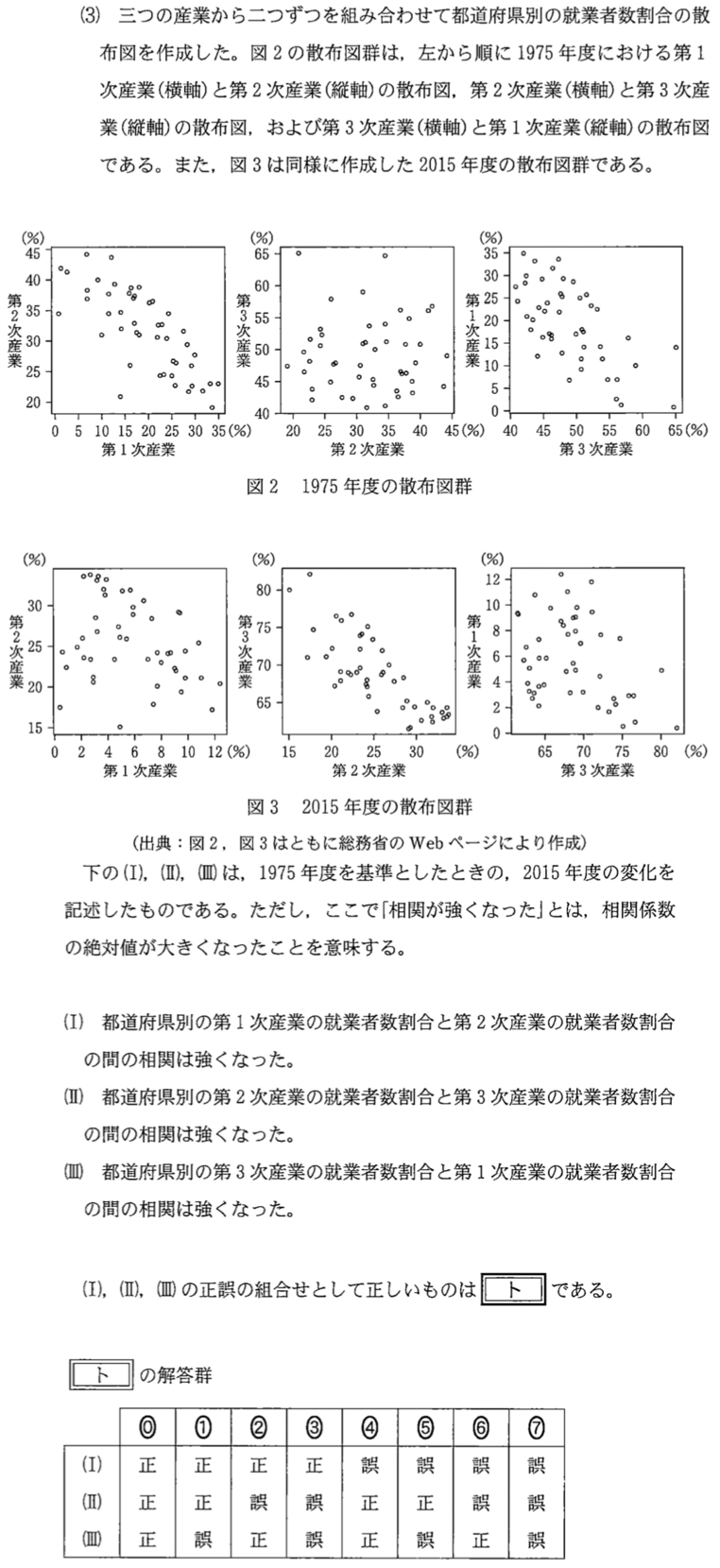
(3)解答・解説《ト》
図 \(2\)の左の散布図は負の相関があるが,図 \(3\) の左の散布図には相関が見られない.よって相関は弱くなっているため,( Ⅰ ) は誤りである.
図 \(2\)の真ん中の散布図には相関が見られないが,図 \(3\) の真ん中の散布図は負の相関がある.よって相関は強くなっているため,( Ⅱ ) は正しい.
図 \(2\)の右の散布図は負の相関があるが,図 \(3\) の右の散布図には相関が見られない.よって相関は弱くなっているため,( Ⅲ ) は誤りである.
したがって,( Ⅰ ) 誤,( Ⅱ ) 正,( Ⅲ ) 誤 ・・・《ト:⑤》
(4)問題と解答・解説《ナ》
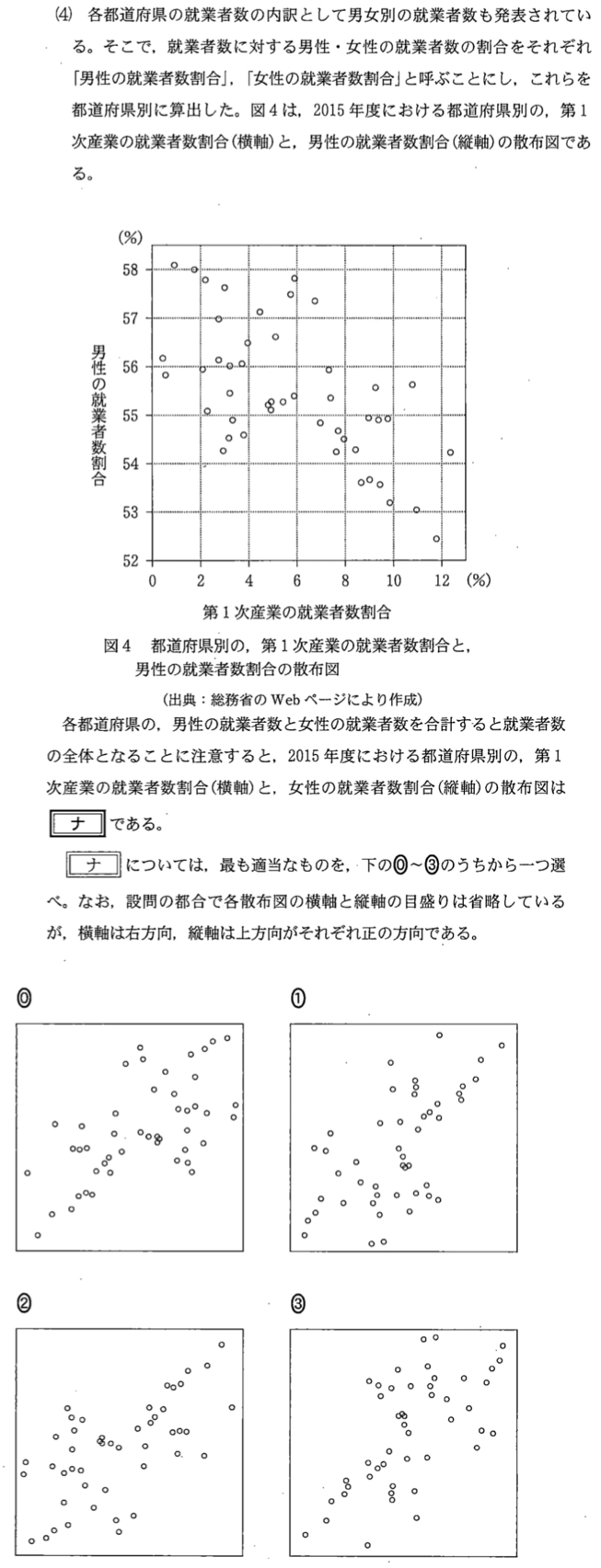
(4)解答・解説《ナ》
男性と女性の就業者割合の和は \(100\) %となるから,男性の就業者数割合の散布図と上下逆になった散布図を選べば良いので,求める女性の就業者数割合の散布図は②・・・《ナ》









コメント