【2003東京大学】
円周率が \(3.05\) より大きいことを証明せよ。
円周率とは？
円周率 \(\pi\) とな何か説明できますか？？
\(\pi=3.14\cdots\) とずっと続く値ですよね・・・？
改めて聞かれると何と答えたらよいのか・・・。
この有名問題を機に，円周率の定義を確認しておきましょう！
解答・解説
円周率 \(\pi\) とは円の直径に対する円周の長さの比である．よって円周率 \(\pi\) は，直径 \(1\) の円の周の長さでもある．
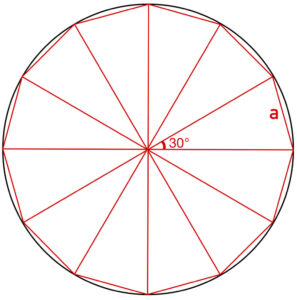ここで円周の長さは，その円に内接する多角形の辺の長さの総和より大きいので，直径が \(1\) の円に内接する正十二角形を考える．
この正十二角形の \(1\) 辺の長さを \(a\) とすると余弦定理より
\(a^2=\left(\displaystyle\frac{1}{2}\right)^2+\left(\displaystyle\frac{1}{2}\right)^2-2\times \left(\displaystyle\frac{1}{2}\right)^2\cos 30°\)
\(a^2=\displaystyle\frac{2-\sqrt{3}}{4}\)
\(a=\displaystyle\frac{\sqrt{2-\sqrt{3}}}{2}=\displaystyle\frac{1}{2}\sqrt{\displaystyle\frac{4-2\sqrt{2}}{2}}=\displaystyle\frac{\sqrt{(\sqrt{3}-1)^2}}{2\sqrt{2}}=\displaystyle\frac{\sqrt{6}-\sqrt{2}}{4}\)
よって，\(\pi>12a=3(\sqrt{6}-\sqrt{2})\)
ここで，\(6>2.44^2=5.9536\) ，\(2<1.42^2=2.0164\) より
\(\sqrt{6}>2.44\) ，\(\sqrt{2}<1.42\) であるから
\(\pi>3(\sqrt{6}-\sqrt{2})>3(2.44-1.42)=3.06>3.05\)
したがって，\(\pi>3.05\) が成立する．
コメント