【2023東京大学・理科・第３問】
\(a\) を実数とし，座標平面上の点 \((0,a)\) を中心とする半径 \(1\) の円の周を \(C\) とする．
(１) \(C\) が，不等式 \(y>x^2\) の表す領域に含まれるような \(a\) の範囲を求めよ．
(２) \(a\) は(１)で求めた範囲にあるとする．\(C\) のうち，\(x≧0\) かつ \(y<a\) を満たす部分を \(S\) とする．\(S\) 上の点 \(P\) に対し，点 \(P\) での \(C\) の接線が放物線 \(y=x^2\) によって切り取られてできる線分の長さを \(L_{P}\) とする．\(L_{Q}=L_{R}\) となる \(S\) 上の相異なる \(2\) 点 \(Q\)，\(R\) が存在するような \(a\) の範囲を求めよ．
解答・解説
(１) \(C\) が \(y>x^2\) の表す領域に含まれるような \(a\) の範囲
\(C\) 上の任意の点 \((x,y)\) は \(0≦\theta<2\pi\) として
\(x=\cos \theta\) ，\(y=a+\sin \theta\) とおける．
\((\cos \theta,a+\sin \theta)\) が \(y>x^2\) を満たすとき
\(a+\sin \theta>\cos^2\theta=1-\sin^2 \theta\)
\(a>-\sin^2 \theta-\sin\theta+1=-\left(\sin \theta+\displaystyle\frac{1}{2}\right)^2+\displaystyle\frac{5}{4}\)
ゆえに求める範囲は，\(a>\displaystyle\frac{5}{4}\)
(２) \(L_{Q}=L_{R}\) となる \(S\) 上の相異なる \(2\) 点 \(Q\)，\(R\) が存在するような \(a\) の範囲
\(S\) 上の任意の点 \(P\) の座標は \(-\displaystyle\frac{\pi}{2}≦ \theta<0\) として
\(x=\cos \theta\) ，\(y=a+\sin \theta\) とおける．
このとき，点 \(P\) における \(C\) の接線は
\(x\cdot\cos \theta+(y-a)\cdot\sin\theta=1\)
\(-\displaystyle\frac{\pi}{2}≦ \theta<0\) のとき \(\sin\theta\not=0\) より
\(y=-\displaystyle\frac{\cos\theta}{\sin\theta}x+a+\displaystyle\frac{1}{\sin\theta}\) ・・・①
①と \(y=x^2\) の共有点は
\(x^2=-\displaystyle\frac{\cos\theta}{\sin\theta}x+a+\displaystyle\frac{1}{\sin\theta}\)
\(x^2+\displaystyle\frac{\cos\theta}{\sin\theta}x-a-\displaystyle\frac{1}{\sin\theta}=0\) ・・・②
\(a>\displaystyle\frac{5}{4}\) のとき②は異なる \(2\) つの実数解をもつので，
②の \(2\) 解を \(x=\alpha,\beta\) ( \(\alpha<\beta\) ) とおくと
解と係数の関係から
\(\alpha+\beta=-\displaystyle\frac{\cos\theta}{\sin\theta}\)，\(\alpha\beta=-a-\displaystyle\frac{1}{\sin \theta}\)
\((\beta-\alpha)^2=(\alpha+\beta)^2-4\alpha\beta\)
\(=\displaystyle\frac{\cos^2\theta}{\sin^2\theta}+4\left(a+\displaystyle\frac{1}{\sin \theta}\right)\)
\(=\displaystyle\frac{1}{\sin^2\theta}+\displaystyle\frac{4}{\sin\theta}+4a-1\) ・・・③
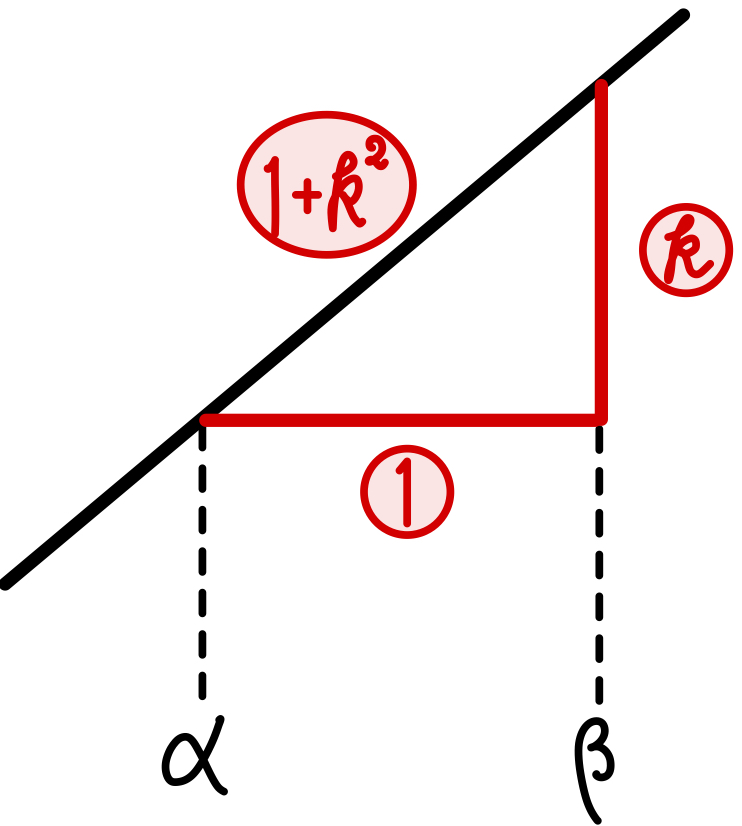傾き \(k\) の直線において，
\(x=\alpha\) から \(\beta\) までの線分の長さ \(L\) は
\(L=(\beta-\alpha)\sqrt{1+k^2}\)
ここで①より接線の傾きは \(-\displaystyle\frac{\cos \theta}{\sin \theta}\) より
\(L_{P}^2=(\beta-\alpha)^2\left\{1+\left(-\displaystyle\frac{\cos \theta}{\sin \theta}\right)^2\right\}=\displaystyle\frac{(\beta-\alpha)^2}{\sin^2 \theta}\)
③より
\(L_{P}^2=\displaystyle\frac{1}{\sin^4\theta}+\displaystyle\frac{4}{\sin^3\theta}+\displaystyle\frac{4a-1}{\sin^2\theta}\)
ここで \(t=\displaystyle\frac{1}{\sin \theta}\) とおくと
\(-\displaystyle\frac{\pi}{2}≦ \theta<0\) より \(t≦-1\)
\(L_{P}^2=t^4+4t^3+(4a-1)t^2=f(t)\) とおく．
\(L_{P}>0\) で \(\theta\) と \(t\) は \(1\) 対 \(1\) に対応することに注目すると
題意を満たす条件は
「\(t≦-1\) において，\(f(t_{1})=f(t_{2})\) をみたす異なる \(t_{1}\)，\(t_{2}\) が存在する 」
つまり，「\(t<-1\) で \(f(t)\) が極値をもつ」
\(f^{\prime}(t)=4t^3+12t^2+2(4a-1)t\)
\(=2t\left\{2t^2+6t+(4a-1)\right\}\) なので
\(2t^2+6t+4a-1\) が \(t<-1\) の範囲で符号変化がおこればよい
\(g(t)=2t^2+6t+4a-1\) とおく
\(g(t)=2\left(t+\displaystyle\frac{3}{2}\right)^2-\displaystyle\frac{11}{2}+4a\)
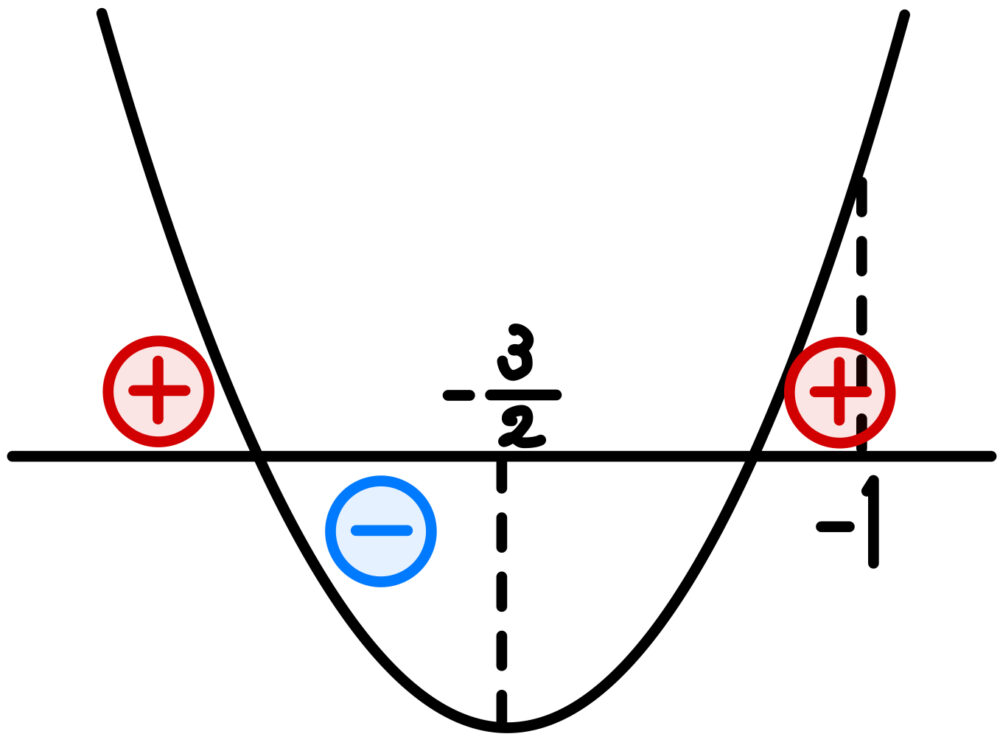軸 \(t=-\displaystyle\frac{3}{2}<-1\)
\(g(-1)=4a-5>0\) ( ∵ (１) より \(a>\displaystyle\frac{5}{4}\) )
よって \(g\left(-\displaystyle\frac{3}{2}\right)<0\) を満たせばよい．
\(g\left(-\displaystyle\frac{3}{2}\right)=-\displaystyle\frac{11}{2}+4a<0\)
\(a<\displaystyle\frac{11}{8}\)
(１) より \(a>\displaystyle\frac{5}{4}\) なので
\(\displaystyle\frac{5}{4}<a<\displaystyle\frac{11}{8}\)
コメント