【2023九州大学・理系・第5問】
\(xy\) 平面上の曲線 \(C\) を,媒介変数 \(t\) を用いて次のように定める.
\(x=t+2\sin^2 t\) ,\(y=t+\sin t\) ( \(0<t<\pi\) )
以下の問いに答えよ.
(1) 曲線 \(C\) に接する直線のうち \(y\) 軸と平行なものがいくつあるか求めよ.
(2) 曲線 \(C\) のうち \(y≦x\) の領域にある部分と直線 \(y=x\) で囲まれた図形の面積を求めよ.
解答・解説
(1) 曲線 \(C\) に接する直線のうち \(y\) 軸と平行なものがいくつあるか
\(\displaystyle\frac{dx}{dt}=1+4\sin t\cos t=1+2\sin 2t\)
\(\displaystyle\frac{dy}{dt}=1+\cos t\)
\(0<t<\pi\) より \(1+\cos t>0\) より
\(\displaystyle\frac{dx}{dy}=\displaystyle\frac{1+2\sin 2t}{1+\cos t}\)
曲線 \(C\) に接する直線のうち \(y\) 軸と平行になるのは
\(\displaystyle\frac{dx}{dy}=0\) \(\iff\) \(\displaystyle\frac{1+2\sin 2t}{1+\cos t}=0\)
\(\iff\) \(\sin 2t=-\displaystyle\frac{1}{2}\)
\(0<t<\pi\) より \(0<2t<2\pi\) なので
\(2t=\displaystyle\frac{7\pi}{6},\displaystyle\frac{11\pi}{6}\)
よって,\(t=\displaystyle\frac{7\pi}{12},\displaystyle\frac{11\pi}{12}\)

\(t\) の値が \(2\) つだからと言って,接線が \(2\) 本あるというのは危険!!
\(t=\displaystyle\frac{7\pi}{12},\displaystyle\frac{11\pi}{12}\) のとき,接線が一致する可能性もあるため,それぞれ代入して確認を行うように!
\(t=\displaystyle\frac{7\pi}{12}\) のとき
\(x=\displaystyle\frac{7\pi}{12}+2\sin^2 \displaystyle\frac{7\pi}{12}=\displaystyle\frac{7\pi}{12}+1-2\cos \displaystyle\frac{7\pi}{6}=\displaystyle\frac{7\pi}{12}+1+\sqrt{3}\)
\(t=\displaystyle\frac{11\pi}{12}\) のとき
\(x=\displaystyle\frac{11\pi}{12}+2\sin^2 \displaystyle\frac{11\pi}{12}=\displaystyle\frac{11\pi}{12}+1-2\cos \displaystyle\frac{11\pi}{6}=\displaystyle\frac{11\pi}{12}+1-\sqrt{3}\)
となり,\(t=\displaystyle\frac{7\pi}{12},\displaystyle\frac{11\pi}{12}\) における \(y\) 軸に平行な接線は一致しない.したがって,求める接線は \(2\) 本ある.
(2) 曲線 \(C\) のうち \(y≦x\) の領域にある部分と直線 \(y=x\) で囲まれた図形の面積
| \(t\) | \(( 0 )\) | ・・・ | \(\displaystyle\frac{7\pi}{12}\) | ・・・ | \(\displaystyle\frac{11\pi}{12}\) | ・・・ | \(( \pi )\) |
| \(\displaystyle\frac{dx}{dt}\) | + | \(0\) | ー | \(0\) | + | ||
| \(\displaystyle\frac{dy}{dt}\) | + | + | + | + | + | ||
| \((x,y)\) | ↗️ | ↖️ | ↗️ |
また,\(t+\sin t≦t+2\sin^2 t\) のとき
\(2\sin t\left(\sin t-\displaystyle\frac{1}{2}\right)≧0\)
\(\iff\) \(\sin t≦0,\displaystyle\frac{1}{2}≦\sin t\)
\(0<t<\pi\) より \(\displaystyle\frac{\pi}{6}≦t≦\displaystyle\frac{5\pi}{6}\)
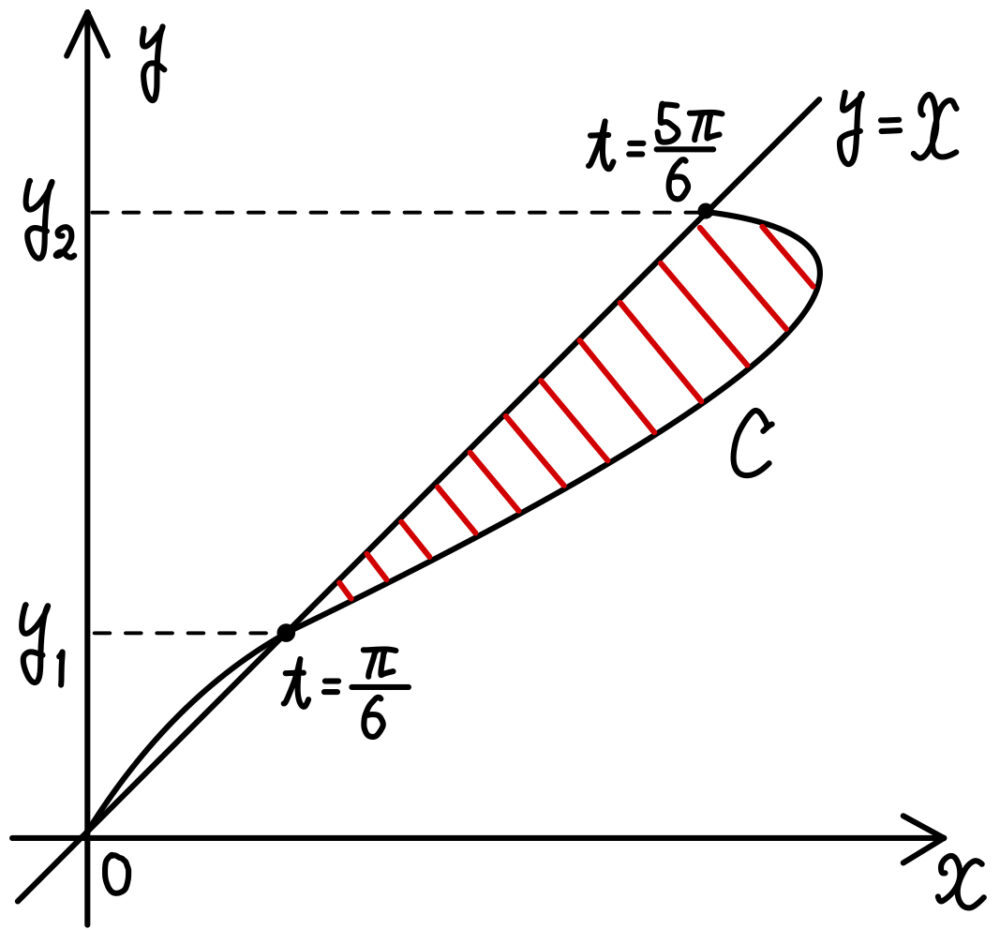 したがって,求める面積は右図の斜線部分.
したがって,求める面積は右図の斜線部分.
右図のように \(y_{1}\),\(y_{2}\) をとる.
求める斜線部分の面積は
\(\displaystyle\int^{y_{2}}_{y_{1}}\left\{(t+2\sin^2 t)-(t+\sin t)\right\} dy\)
\(=\displaystyle\int^{\frac{5\pi}{6}}_{\frac{\pi}{6}}(2\sin^2 t-\sin t) \displaystyle\frac{dy}{dt}dt\)
\(=\displaystyle\int^{\frac{5\pi}{6}}_{\frac{\pi}{6}}(2\sin^2 t-\sin t)(1+\cos t)dt\)
\(=\displaystyle\int^{\frac{5\pi}{6}}_{\frac{\pi}{6}}(2\sin^2t+2\sin^2t\cos t-\sin t-\sin t\cos t)dt\)
\(=\displaystyle\int^{\frac{5\pi}{6}}_{\frac{\pi}{6}}(1-\cos 2t+2\sin^2t\cos t-\sin t-\sin t\cos t)dt\)
\(=\Bigl[t-\displaystyle\frac{1}{2}\sin 2t+\displaystyle\frac{2}{3}\sin^3t+\cos t-\displaystyle\frac{1}{2}\sin^2 t\Bigr]^{\frac{5\pi}{6}}_{\frac{\pi}{6}}\)
\(=\displaystyle\frac{2\pi}{3}-\displaystyle\frac{\sqrt{3}}{2}\)







コメント