【2022数学ⅠA】第4問(整数の性質)
(1)問題と解答・解説《ア〜ク》

解答・解説《ア〜ク》
\(5^4=625\) を \(2^4=16\) で割ると
商は \(39\) , 余りは \(1\) であるから
\(5^4=2^4\times 39+1\)
\(\iff\) \(5^4\times 1-2^4\times 39=1\)
よって,\(5^4x-2^4y=1\) ・・・① の整数解のうち
\(x\) が正の整数で最小になるのは
\(x=1\) , \(y=39\) ・・・《ア〜ウ》

\(5^4x-2^4y=1\) ・・・① の整数解は
直線 \(y=\displaystyle\frac{5^4}{2^4}x-\displaystyle\frac{1}{2^4}\) 上の格子点を表す.
\((1,39)\) は格子点の \(1\) つより,整数 \(k\) を用いて
\(x=2^4k+1\) , \(y=5^4k+39\) が①の整数解となる.
これらの中で,\(x\) が \(2\) 桁の正の整数で最小になるのは \(k=1\) のとき
このとき,\(x=17\) , \(y=664\) ・・・《エ〜ク》
(2)問題と解答・解説《ケ〜コ》
解答・解説《ケ〜コ》
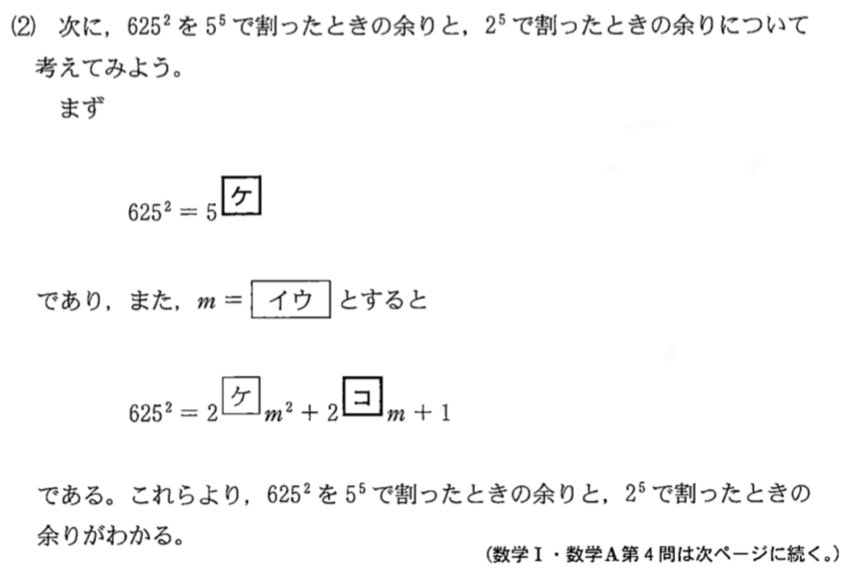
\(625^2=\left(5^4\right)^2=\)\(5^8\) ・・・《ケ》
(1)より \(5^4=2^4\times 39+1\) より,\(m=39\) とすると
\(5^4=2^4m+1\)
これを \(2\) 乗すると
\(\left(5^4\right)^2=(2^4m+1)^2\)
\(625^2=2^8m^2+2^5m+1\) ・・・《コ》
これより,\(625^2\) を \(5^5\) で割ったときの余りは \(0\) , \(2^5\) で割ったときの余りは \(1\) である.
(3)問題と解答・解説《サ〜ツ》

解答・解説《サ〜ツ》
\(5^5x-2^5y=1\) ・・・② より
\(5^5x=2^5y+1\) であるから
\(5^5x\) を \(5^5\) で割ったときの余りは \(0\) , \(2^5\) で割ったときの余りは \(1\) である.
また(2) の結果から,
\(5^5x-625^2\) は \(5^5\) かつ \(2^5\) で割り切れる.
\(5^5\) と \(2^5\) は互いに素であるから,\(5^5x-625^2\) は \(5^5\times 2^5\) の倍数となる.
よって整数 \(l\) を用いて
\(5^5x-625^2=5^5\times 2^5l\)・・・③
③の両辺を \(5^5\) で割ると
\(x-5^3=2^5l\)
②の整数解のうち,\(x\) が \(3\) 桁の正の整数で最小となるのは,\(l=0\) のとき
このとき,\(x=125\) ・・・《サ〜ス》
②より
\(5^5\times 125-2^5y=1\) \(\iff\) \(y=12207\) ・・・《セ〜ツ》
(4)問題と解答・解説《テ〜ノ》

解答・解説《テ〜ノ》

試験本番であれば、この問題は後回し(または捨てる)すべき問題です!
共通テストは時間との勝負でもありますので、他の問題に時間を使いましょう!
(4)については、「2022共通テスト整数「11^5x-2^5y=1」誘導なし(1次不定方程式・合同式・パスカルの三角形)」を参考にしてください!










コメント