【2023関西学院大学・全学日程・文系・第１問(１)】
\(a\) を正の実数とし，\(2\) 次関数 \(y=-x^2+6x\) の \(a≦x≦2a\) における最大値を \(M\)，最小値を \(m\) とする．
( ⅰ ) \(a=2\) のとき，\(M-m=\)[ ア ] である．
( ⅱ ) \(M≧0\) であるとき，\(a\) の取りうる値の範囲は [ イ ] である．
( ⅲ ) \(M-m=12\) のとき，\(a=\)[ ウ ] である．
解答・解説
( ⅰ ) \(a=2\) のとき，\(M-m\)
\(y=-x^2+6x=-(x-3)^2+9\)
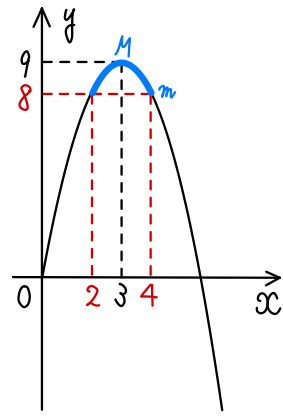
\(a=2\) のとき，\(2≦x≦4\) における最大，最小値は
\(x=3\) のとき，最大値：\(M=9\)
\(x=2,4\) のとき，最大値：\(M=8\)
よって，\(M-m=1\) ・・・[ ア ]
( ⅱ ) \(M≧0\) であるとき，\(a\) の取りうる値の範囲
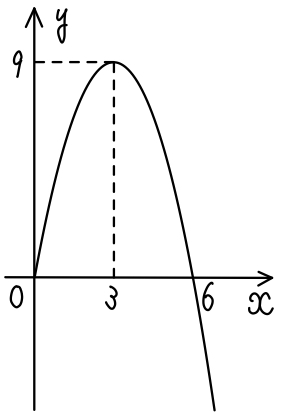
\(x≧0\) における \(y=-x^2+6x=-(x-3)^2+9\)
のグラフは右図のようになるので
\(0≦x≦6\) のとき常に \(y≧0\)
よって，\(M≧0\) となるのは，\(0<a≦6\) ・・・[ イ ]
( ⅲ ) \(M-m=12\) のとき，\(a\) の値
\(0≦x≦6\) における \(y=-x^2+6x\) のグラフは
\(0≦y≦9\) より，\(M-m≦9\) となる．
つまり，\(0<2a≦6\) \(\iff\) \(0<a≦3\) のとき不適．
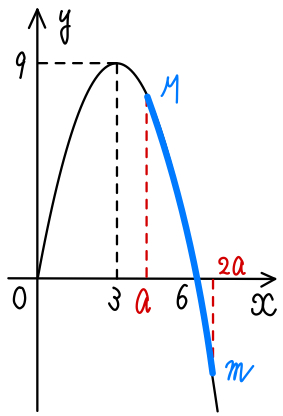
\(a>3\) のとき
\(x=a\) のとき，最大値：\(M=-a^2+6a\)
\(x=2a\) のとき，最大値：\(M=-4a^2+12a\)
\(M-m=(-a^2+6a)-(-4a^2+12a)=3a^2-6a\)
\(M-m=12\) のとき
\(3a^2-6a=12\) \(\iff\) \(a^2-2a-4=0\)
\(a=1\pm\sqrt{5}\)
\(a>3\) より，\(a=1+\sqrt{5}\) ・・・[ ウ ]
コメント