【2023鳥取大学・医学部・第3問】
\(xy\) 平面上において,曲線 \(C\) : \(y=\sqrt{x}\) と直線 \(l\) : \(y=x\) を考える.以下の問いに答えよ.
(1) \(C\) と \(l\) で囲まれる図形の面積を求めよ.
(2) 曲線 \(C\) 上の点 \(P(x,\sqrt{x})\) ( \(0≦x≦1\) ) に対し,点 \(P\) から直線 \(l\) に下ろした垂線と,直線 \(l\) との交点を \(Q\) とする.線分 \(PQ\) の長さを \(x\) を用いて表せ.
(3) \(C\) と \(l\) で囲まれる図形を直線 \(l\) の周りに一回転してできる立体の体積を求めよ.
\(y=x\) の周りに一回転してできる立体の体積
傘型分割の積分
\(y=f(x)\) と \(y=x\) で囲まれた部分を \(y=x\) の周りに一回転してできる立体の体積 \(V\) は
\(V=\displaystyle\int^{b}_{a}\pi\left(\displaystyle\frac{x-f(x)}{\sqrt{2}}\right)^2 \sqrt{2}dx\)
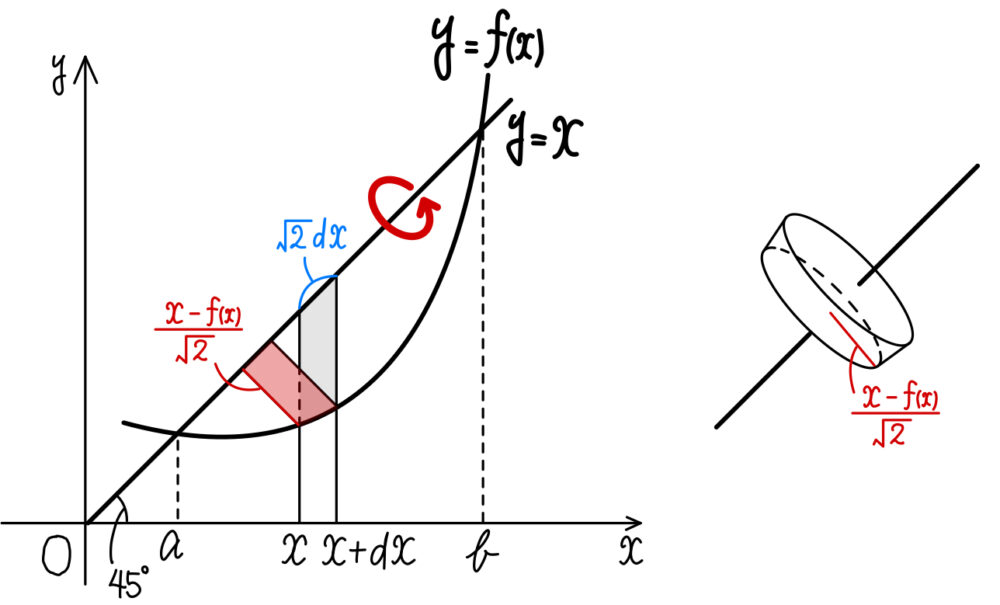

上図のようなイメージを持っておきましょう!
右図のような円柱を寄せ集めすることで,求める体積を求めることができます!
解答・解説
(1) \(C\) と \(l\) で囲まれる図形の面積
\(y=\sqrt{x}\) ( \(x≧0\) ) と \(y=x\) の交点の \(x\) 座標は
\(\sqrt{x}=x\) \(\iff\) \(x=x^2\)
\(\iff\) \(x(x-1)=0\)
\(x=0,1\)
よって求める面積は
\(\displaystyle\int^{1}_{0}\left(\sqrt{x}-x\right) dx=\Bigl[\displaystyle\frac{2}{3}x^{\frac{3}{2}}-\displaystyle\frac{1}{2}x^2\Bigr]^{1}_{0}=\displaystyle\frac{1}{6}\)
(2) 線分 \(PQ\) の長さを \(x\) を用いて表せ.
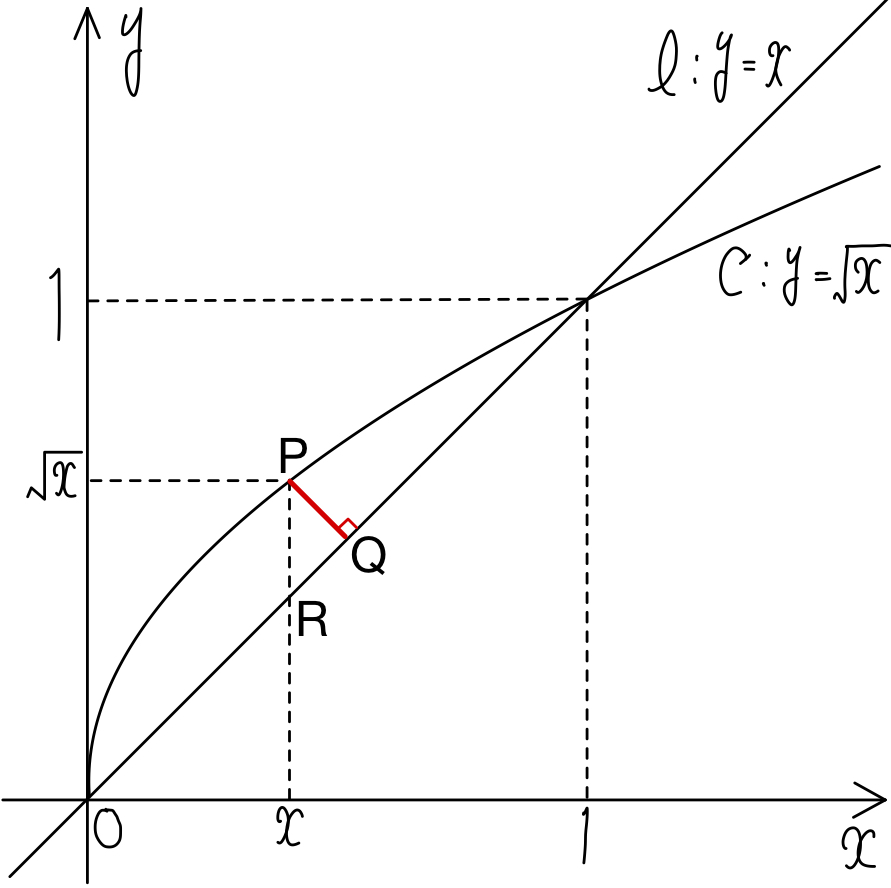
\(R(x,x)\) とおくと,
\(PQ=\displaystyle\frac{PR}{\sqrt{2}}=\displaystyle\frac{\sqrt{x}-x}{\sqrt{2}}\)
(3) \(C\) と \(l\) で囲まれる図形を直線 \(l\) の周りに一回転してできる立体の体積
求める体積は
\(\displaystyle\int^{1}_{o}\pi\left(\displaystyle\frac{\sqrt{x}-x}{\sqrt{2}}\right)^2\cdot\sqrt{2}dx\)
\(=\displaystyle\frac{\sqrt{2}}{2}\pi \displaystyle\int^{1}_{0}\left(x-2x\sqrt{x}+x^2\right) dx\)
\(=\displaystyle\frac{\sqrt{2}}{2}\pi\Bigl[\displaystyle\frac{1}{2}x^2-\displaystyle\frac{4}{5}x^{\frac{5}{2}}+\displaystyle\frac{1}{3}x^3\Bigr]^{1}_{0}\)
\(=\displaystyle\frac{\sqrt{2}\pi}{60}\)








コメント