【2002京都大学】アルキメデスの螺旋｜極方程式r=θの曲線の長さ

【2002京都大学・第４問】

(１)　\(x≧0\) で定義された関数 \(f(x)=\log\left(x+\sqrt{1+x^2}\right)\) について，導関数 \(f^{\prime}(x)\) を求めよ．

(２)　極方程式 \(r=\theta\) ( \(\theta≧0\) ) で定義される曲線の，\(0≦\theta≦\pi\) の部分の長さを求めよ．

アルキメデスの螺旋の極方程式
曲線の長さについて
1. 媒介変数された曲線の長さ
2. 曲線 \(y=f(x)\) の長さ
解答・解説
1. (１)
2. (２)

アルキメデスの螺旋の極方程式

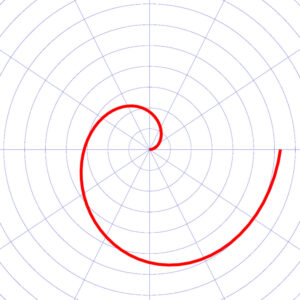
極方程式 \(r=\theta\) ( \(0≦\theta≦2\pi\) ) の部分を点をとってグラフをかくと，右図のような赤曲線になる．

とても有名なグラフになりますので，概形だけでも知っておきましょう！

また，極方程式については

「」

をご参考に！

曲線の長さについて

京都大学では、2009年、2021年にも曲線の長さが出題されています！

しっかりと対策を！

媒介変数された曲線の長さ

曲線 \(x=f(t)\) , \(y=g(t)\) ( \(\alpha≦t≦\beta\) ) の長さ \(L\) は

\(L=\displaystyle\int^{\beta}_{\alpha}\sqrt{\left(\displaystyle\frac{dx}{dt}\right)^2+\left(\displaystyle\frac{dy}{dt}\right)^2} dt=\displaystyle\int^{\beta}_{\alpha}\sqrt{\left\{f^{\prime}(t)\right\}^2+\left\{g^{\prime}(t)\right\}^2} dt\)

【2009京都大学】極方程式、媒介変数、曲線の長さ｜r=1+cosθ(0≦θ≦π)

極方程式r=1+cosθの0≦θ≦πの部分の曲線の長さについて。媒介変数表示し、積分を用いて計算(三角関数の積分)。この１問で、三角関数の公式(加法定理、半角、倍角など)、積分、極方程式、媒介変数など様々なことが復習できる良問。2009年京大、理系、過去問演習、対策。

曲線 \(y=f(x)\) の長さ

曲線 \(y=f(x)\) ( \(a≦x≦b\) ) の長さ \(L\) は

\(L=\displaystyle\int^{b}_{a}\sqrt{1+\left(\displaystyle\frac{dy}{dx}\right)^2} dx=\displaystyle\int^{b}_{a}\sqrt{1+\left\{f^{\prime}(x)\right\}^2} dx\)

【2021京都大学・理系・第4問】曲線の長さ(数学Ⅲ：積分の応用)

曲線の長さの公式と例題。基本的な公式に当てはめて計算するだけの基礎問題。1/cosxの置換積分の計算も典型・頻出。2021京大(理系)過去問演習・対策。

解答・解説

(１)

\(f(x)=\log\left(x+\sqrt{1+x^2}\right)\) より

\(f^{\prime}(x)=\displaystyle\frac{1}{x+\sqrt{1+x^2}}\left(1+\displaystyle\frac{x}{\sqrt{1+x^2}}\right)=\displaystyle\frac{1}{\sqrt{1+x^2}}\)

(２)

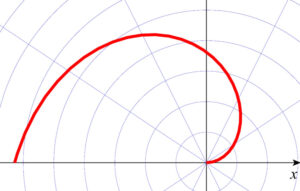曲線 \(r=\theta\) ( \(\theta≧0\) ) 上の点の座標は，極方程式の定義から

\(x=\theta\cos \theta\) ，\(y=\theta\sin \theta\)

よって，

\(\displaystyle\frac{dx}{d\theta}=\cos \theta- \theta\sin \theta\)

\(\displaystyle\frac{dy}{d\theta}=\sin \theta+ \theta\cos \theta\) であるから

\(\left(\displaystyle\frac{dx}{d\theta}\right)^2+\left(\displaystyle\frac{dy}{d\theta}\right)^2=(\cos \theta- \theta\sin \theta)^2+(\sin \theta+ \theta\cos \theta)^2=1+ \theta^2\)

ゆえに求める曲線の長さを \(L\) とすると，

\(L=\displaystyle\int^{\pi}_{0}\sqrt{\left(\displaystyle\frac{dx}{d\theta}\right)^2+\left(\displaystyle\frac{dy}{d\theta}\right)^2} d\theta\)

\(=\displaystyle\int^{\pi}_{0} \sqrt{1+\theta^2}d \theta\)

\(=\Bigl[ \theta\sqrt{1+ \theta^2}\Bigr]^{\pi}_{0}-\displaystyle\int^{\pi}_{0}\displaystyle\frac{\theta^2}{\sqrt{1+\theta^2}} d \theta\)

\(=\pi\sqrt{1+\pi^2}-\displaystyle\int^{\pi}_{0}\left(\sqrt{1+ \theta^2}-\displaystyle\frac{1}{\sqrt{1+\theta^2}}\right)d\theta\)

\(=\pi\sqrt{1+\pi^2}-L+\Bigl[\log\left(\theta+\sqrt{1+\theta^2}\right)\Bigr]^{\pi}_{0}\)

(１)の結果を利用しました！

したがって，

\(L=\displaystyle\frac{1}{2}\left\{\pi\sqrt{1+\pi^2}+\log\left(\pi\sqrt{1+\pi^2}\right)\right\}\)