【2020数学ⅡB：第４問ベクトル】
(１)問題と解答・解説
(１)解答・解説《ア〜カ》
\(\overrightarrow{OA}=3(1,1,-2)\) より
\(\left|\overrightarrow{OA}\right|=3\sqrt{1^2+1^2+(-2)^2}=\)\(3\sqrt{6}\) ・・・《アイ》
\(\overrightarrow{OB}=2(1+\sqrt{3},1-\sqrt{3},-2)\) より
\(\left|\overrightarrow{OB}\right|=2\sqrt{(1+\sqrt{3})^2+(1-\sqrt{3})^2+(-2)^2}=\)\(4\sqrt{3}\) ・・・《ウエ》
\(\overrightarrow{OA}\cdot\overrightarrow{OB}=6\left\{1\times (1+\sqrt{3})+1\times (1-\sqrt{3})+(-2)\times (-2)\right\}=\)\(36\) ・・・《オカ》
(２)問題と解答・解説
(２)解答・解説《キ〜シ》
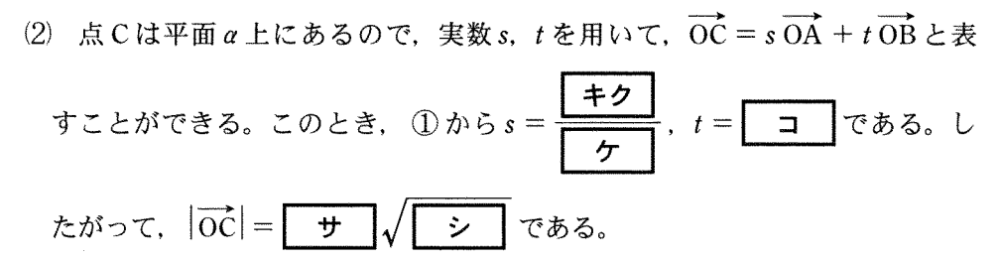
点 \(C\) は平面 \(\alpha\) 上にあるので，実数 \(s\) , \(t\) を用いて \(\overrightarrow{OC}=s\overrightarrow{OA}+t\overrightarrow{OB}\) と表せる．
\(\overrightarrow{OA}\perp\overrightarrow{OC}\) , \(\overrightarrow{OB}\cdot\overrightarrow{OC}=24\) ・・・① より
\(\overrightarrow{OA}\perp\overrightarrow{OC}\) \(\iff\) \(\overrightarrow{OA}\cdot\overrightarrow{OC}=0\)
よって，\(\overrightarrow{OA}\cdot\left(s\overrightarrow{OA}+t\overrightarrow{OB}\right)=0\)
\(s\left|\overrightarrow{OA}\right|^2+t\overrightarrow{OA}\cdot\overrightarrow{OB}=0\)
\(54s+36t=0\) \(\iff\) \(3s+2t=0\) ・・・( ⅰ )
また， \(\overrightarrow{OB}\cdot\overrightarrow{OC}=24\) より
\(\overrightarrow{OB}\cdot\left(s\overrightarrow{OA}+t\overrightarrow{OB}\right)=24\)
\(s\overrightarrow{OA}\cdot\overrightarrow{OB}+t\left|\overrightarrow{OB}\right|^2=24\)
\(36s+48t=24\) \(\iff\) \(3s+4t=2\) ・・・( ⅰⅰ )
( ⅰ )，( ⅰⅰ )より \(s=\displaystyle\frac{-2}{3}\) , \(t=1\) ・・・《キ〜コ》
したがって，\(\overrightarrow{OC}=\displaystyle\frac{-2}{3}\overrightarrow{OA}+\overrightarrow{OB}\) より
\(\left|\overrightarrow{OC}\right|^2=\displaystyle\frac{4}{9}\left|\overrightarrow{OA}\right|^2-\displaystyle\frac{4}{3}\overrightarrow{OA}\cdot\overrightarrow{OB}+\left|\overrightarrow{OB}\right|^2=24\)
よって \(\left|\overrightarrow{OC}\right|=2\sqrt{6}\) ・・・《サシ》
(３)問題と解答・解説
(３)解答・解説《ス〜テ》
\(\overrightarrow{CB}=\overrightarrow{OB}-\overrightarrow{OC}\)
\(=\overrightarrow{OB}-\left(\displaystyle\frac{-2}{3}\overrightarrow{OA}+\overrightarrow{OB}\right)\)
よって，\(\overrightarrow{CB}=\displaystyle\frac{2}{3}\overrightarrow{OA}\) より
\(\overrightarrow{CB}=\displaystyle\frac{2}{3}(3,3,-6)=\)\((2,2,-4)\) ・・・《ス〜タ》
また，\(\overrightarrow{CB}=\displaystyle\frac{2}{3}\overrightarrow{OA}\) より
\(\overrightarrow{CB}\) / / \(\overrightarrow{OA}\) であり，\(\left|\overrightarrow{CB}\right|\not=\left|\overrightarrow{OA}\right|\) であるから
四角形 \(OABC\) は ③平行四辺形でないが，台形である・・・《チ》
ここまでに求めた条件から
\(\left(\overrightarrow{OA}\perp \overrightarrow{OC} ,\left|\overrightarrow{OA}\right|=3\sqrt{6} , \left|\overrightarrow{OC}\right|=2\sqrt{6} , \left|\overrightarrow{CB}\right|=\displaystyle\frac{2}{3}\left|\overrightarrow{OA}\right|=2\sqrt{6} , \overrightarrow{CB} / / \overrightarrow{OA}\right)\)
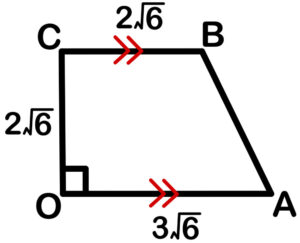求める図形は右図のようになる．
したがって，四角形 \(OABC\) の面積は
\(\triangle ABC+\triangle OAC\)
\(=\displaystyle\frac{1}{2}\cdot 2\sqrt{6}\cdot 2\sqrt{6}+\displaystyle\frac{1}{2}\cdot 2\sqrt{6}\cdot 3\sqrt{6}=\)\(36\) ・・・《ツテ》
(４)問題と解答・解説
(４)解答・解説《ト〜ホ》
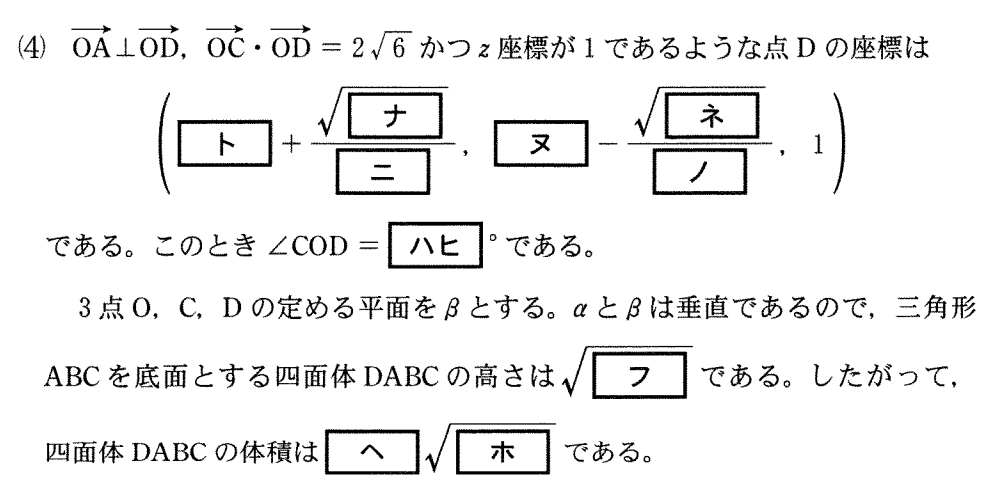
\(D ( x , y , 1 )\) とおく．
\(\overrightarrow{OA}\perp\overrightarrow{OD}\) より \(\overrightarrow{OA}\cdot\overrightarrow{OD}=0\)
\(\iff\) \(3(x+y-2=0)\)
よって，\(x+y=2\) ・・・(※)
また，\(\overrightarrow{OC}=\displaystyle\frac{-2}{3}\overrightarrow{OA}+\overrightarrow{OB}\) より
\(\overrightarrow{OC}=\displaystyle\frac{-2}{3}(3,3,-6)+(2+2\sqrt{3},2-2\sqrt{3},-4)\)
\(=2\sqrt{3}(1,-1,0)\) であり，
\(\overrightarrow{OC}\cdot\overrightarrow{OD}=2\sqrt{6}\) より
\(2\sqrt{6}(x-y)=2\sqrt{6}\)
よって，\(x-y=\sqrt{2}\) ・・・(※※)
(※)，(※※) より \(x=\displaystyle\frac{2+\sqrt{2}}{2}\) , \(y=\displaystyle\frac{2-\sqrt{2}}{2}\)
したがって，\(D\left(1+\displaystyle\frac{\sqrt{2}}{2} , 1-\displaystyle\frac{\sqrt{2}}{2} , 1\right)\) ・・・《ト〜ノ》
次に，\(\left|\overrightarrow{OD}\right|^2=\left(1+\displaystyle\frac{\sqrt{2}}{2}\right)^2+\left(1-\displaystyle\frac{\sqrt{2}}{2}\right)^2+1^2=4\)
よって，\(\left|\overrightarrow{OD}\right|=2\)
また，\(\left|\overrightarrow{OC}\right|=2\sqrt{6}\) , \(\overrightarrow{OC}\cdot\overrightarrow{OD}=2\sqrt{6}\) より
\(\cos \angle COD=\displaystyle\frac{2\sqrt{6}}{2\sqrt{6}\times 2}=\displaystyle\frac{1}{2}\)
\(\cos \angle COD = 60°\) ・・・《ハヒ》
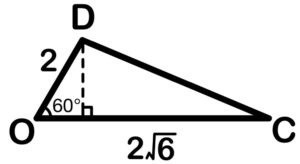
また左図より，
求める四面体の高さは
\(2\sin 60°=\) \(\sqrt{3}\) ・・・《フ》
以上より，求める体積は
\(\displaystyle\frac{1}{3}\times \triangle ABC \times \sqrt{3}=\) \(4\sqrt{3}\) ・・・《ヘホ》
コメント