【2022大阪医科薬科大学・看護・[3]】
解答・解説
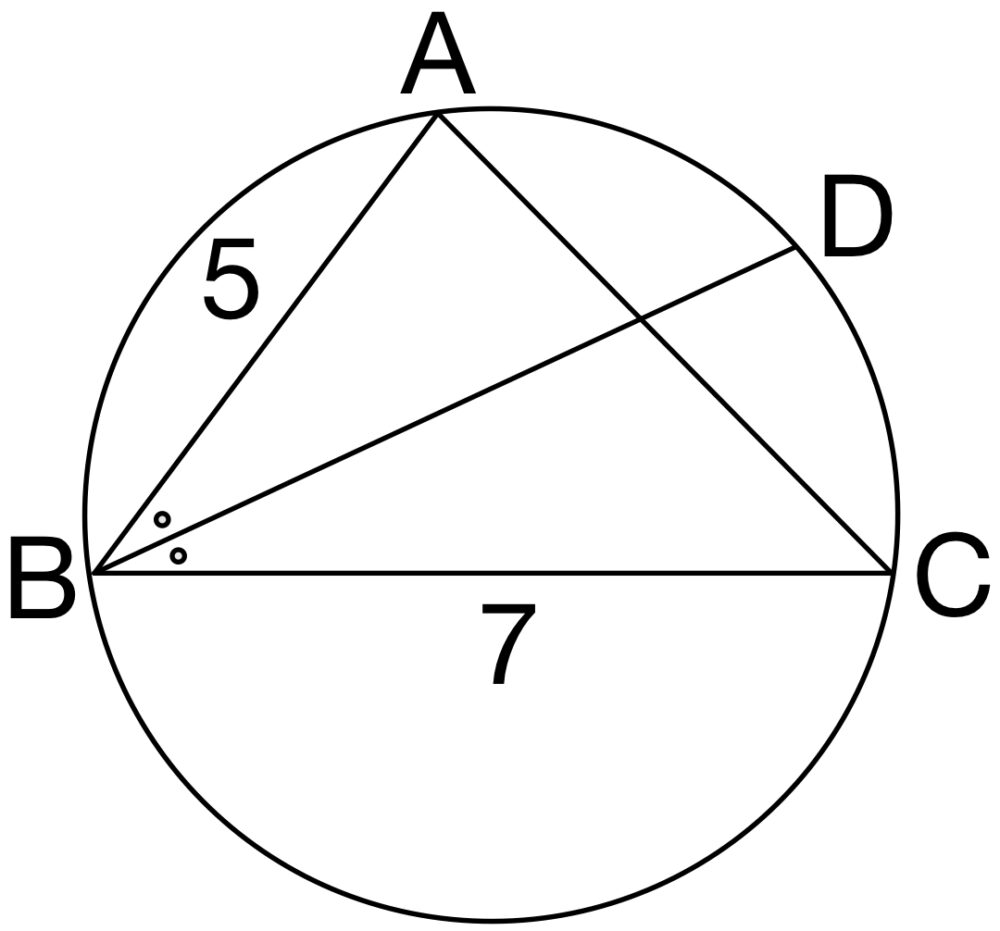
(１) 余弦定理
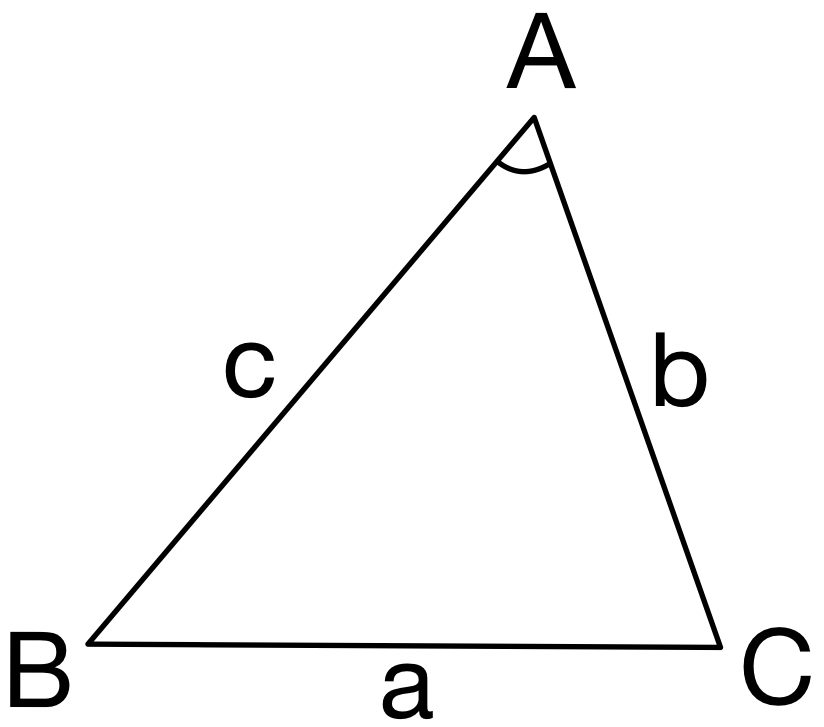余弦定理
\(\triangle ABC\) において
・\(a^2=b^2+c^2-2bc\cos A\)
・\(\cos A=\displaystyle\frac{b^2+c^2-a^2}{2bc}\)
余弦定理より
\(AC^2=5^2+7^2-2\times 5\times 7\times \displaystyle\frac{3}{5}=32\)
\(AC>0\) より \(AC=4\sqrt{2}\) ・・・( b )
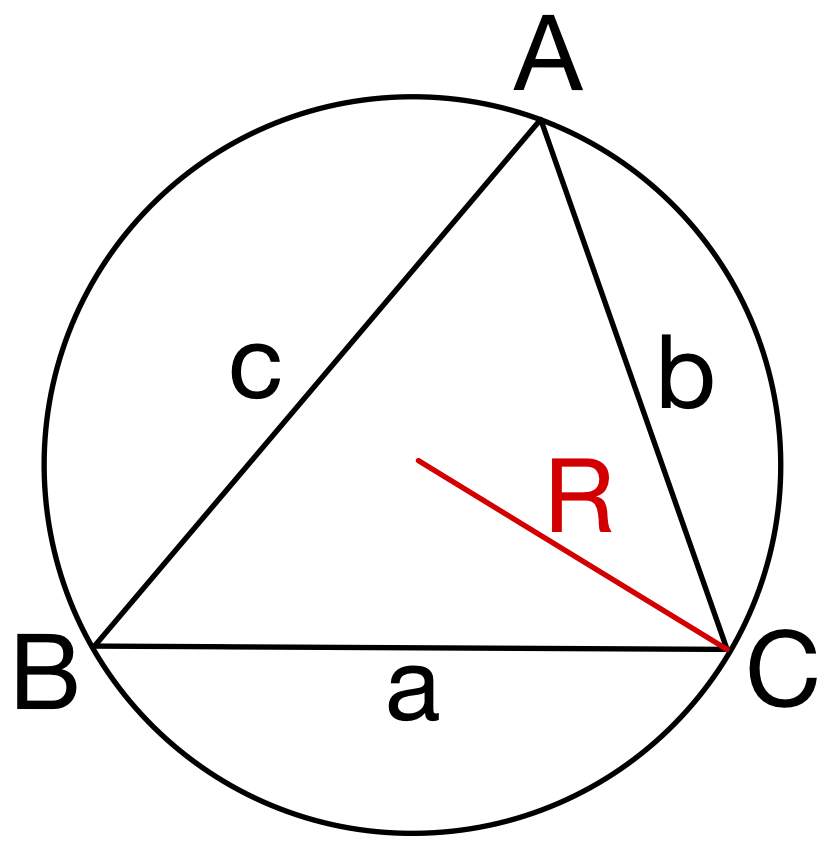(２) 正弦定理
正弦定理
\(\triangle ABC\) の外接円半径を \(R\) とする．
\(2R=\displaystyle\frac{a}{\sin A}=\displaystyle\frac{b}{\sin B}=\displaystyle\frac{c}{\sin C}\)
\(\sin^2 B+\cos^2B=1\) より
\(\sin^2B=1-\left(\displaystyle\frac{3}{5}\right)^2=\displaystyle\frac{16}{25}\)
\(0°<B<180°\) より \(\sin B>0\) なので \(\sin B=\displaystyle\frac{4}{5}\)
正弦定理より
\(2R=\displaystyle\frac{b}{\sin B}=\displaystyle\frac{4\sqrt{2}}{\frac{4}{5}}=5\sqrt{2}\)
よって，\(R=\displaystyle\frac{5\sqrt{2}}{2}\) ・・・( a )
(３) 円に内接する四角形
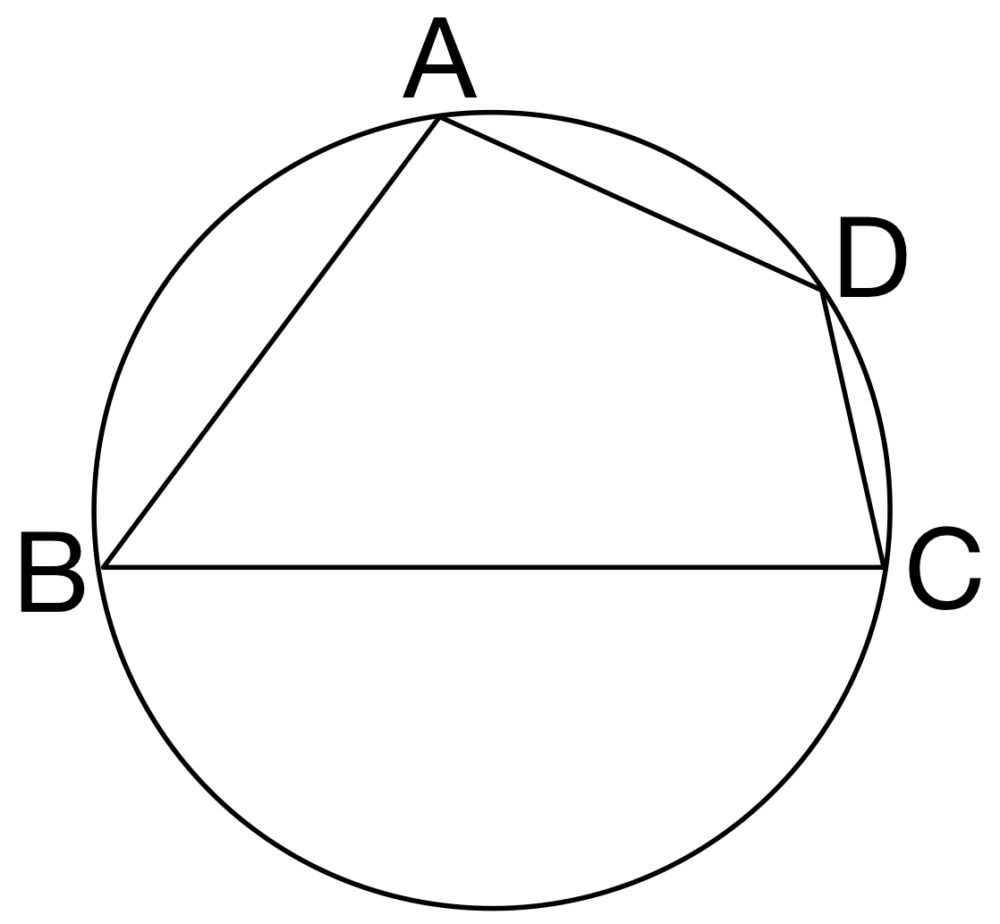円に内接する四角形
・対角の和が 180° ( \(B+D=180°\))
\(D=180°-B\) より
・\(\sin D=\sin(180°-B)=\sin B\)
・\(\cos D=\cos(180°-B)=-\cos B\)
\(\angle ABD=\angle CBD\) より
孤 \(AD=\) 孤 \(CD\)
よって \(AD=CD\) ( \(=x\) とおく )
\(\triangle ACD\) で余弦定理より
\((4\sqrt{2})^2=x^2+x^2-2\cdot x\cdot x\cdot \cos D\)
ここで，\(B+D=180°\) より
\(\cos D=\cos (180°-B)=-\cos B=-\displaystyle\frac{3}{5}\)
よって，\(32=2x^2-2x^2\times \left(-\displaystyle\frac{3}{5}\right)\)
\(\displaystyle\frac{16}{5}x^2=32\) \(\iff\) \(x^2=10\)
\(x>0\) より \(x=\sqrt{10}\) ・・・( d )
(４)
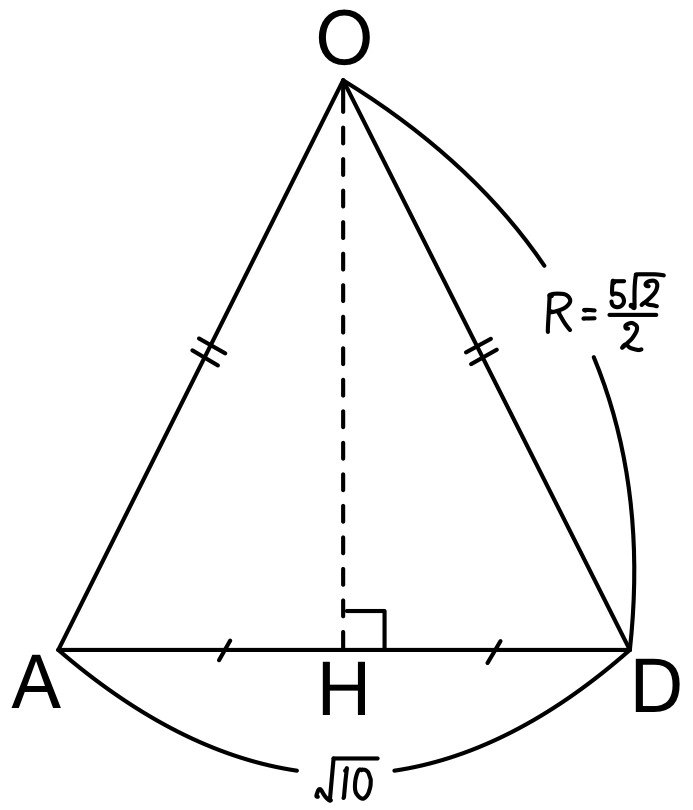\(OA=OD=R\) より
\(\triangle OAD\) は二等辺三角形となる．
点 \(O\) から \(AD\) に下ろした垂線の足を \(H\) とおく．
\(\triangle ODH\) で三平方の定理から
\(OD^2=OH^2+DH^2\)
\(\left(\displaystyle\frac{5\sqrt{2}}{2}\right)^2=OH^2+\left(\displaystyle\frac{\sqrt{10}}{2}\right)^2\)
\(OH^2=10\)
よって \(OH=\sqrt{10}\)
したがって，
\(\triangle OAD=\displaystyle\frac{1}{2}\times AD\times OH=\displaystyle\frac{1}{2}\times \sqrt{10}\times \sqrt{10}\)
\(\triangle OAD=5\) ・・・( c )
コメント