【2018数学ⅡB:第4問ベクトル】
(1)(2)問題と解答・解説
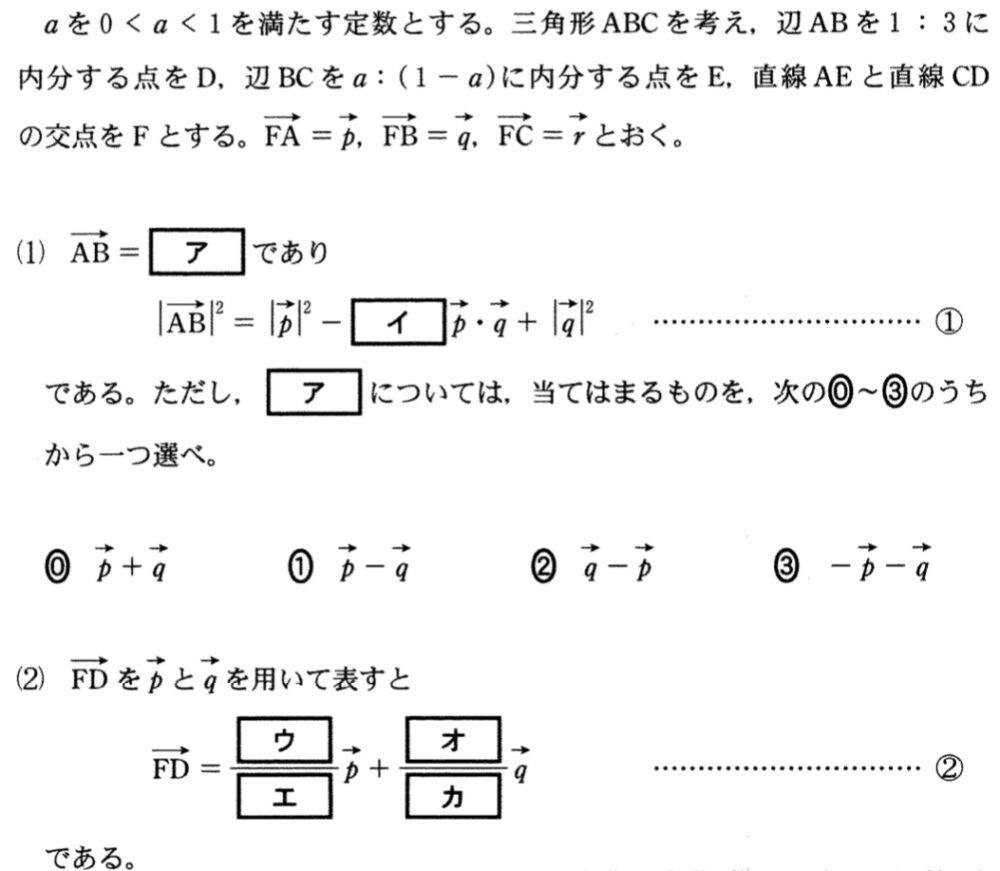
(1)(2)解答・解説《ア〜カ》
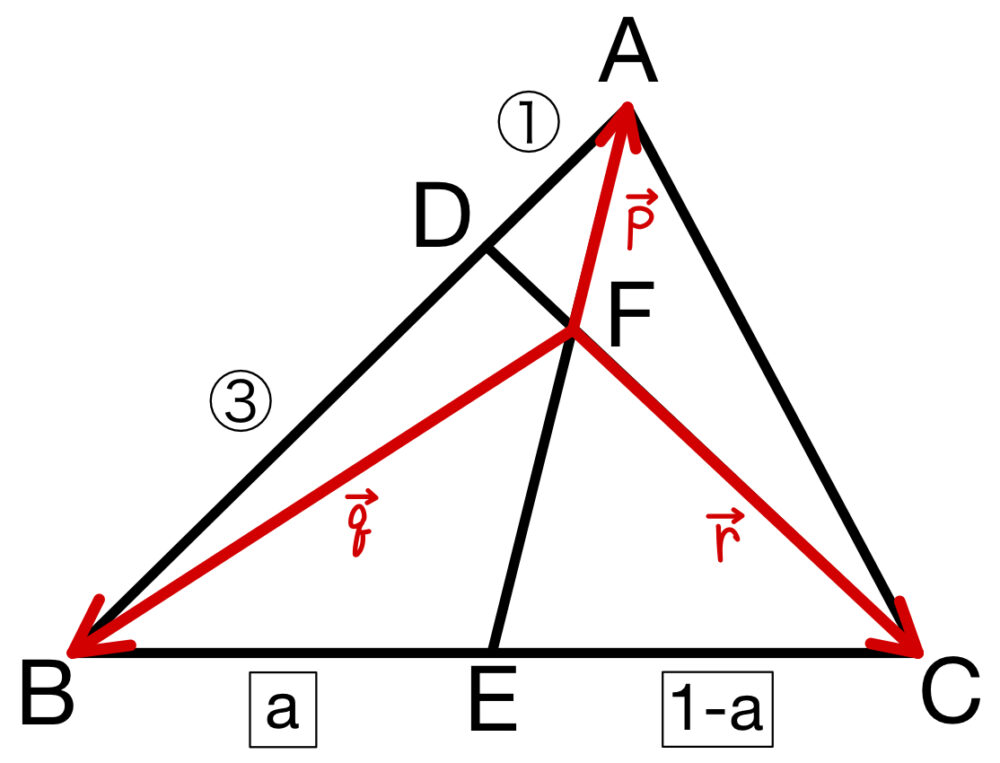
(1) \(\overrightarrow{AB}=\overrightarrow{FB}-\overrightarrow{FA}\)
\(=\overrightarrow{q}-\overrightarrow{p}\) ・・・《ア:②》
より,
\(\left|\overrightarrow{AB}\right|^2=\left|\overrightarrow{q}-\overrightarrow{p}\right|^2\)
\(=\left|\overrightarrow{p}\right|^2-2\overrightarrow{p}\cdot\overrightarrow{q}+\left|\overrightarrow{q}\right|^2\) ・・・①《イ:2》
(2) \(D\) は \(AB\) を \(1 : 3\) に内分する点より
\(\overrightarrow{FD}=\displaystyle\frac{3\overrightarrow{FA}+1\overrightarrow{FB}}{1+3}\)
\(=\displaystyle\frac{3}{4}\overrightarrow{p}+\displaystyle\frac{1}{4}\overrightarrow{q}\) ・・・②《ウ〜カ》
(3)問題と解答・解説
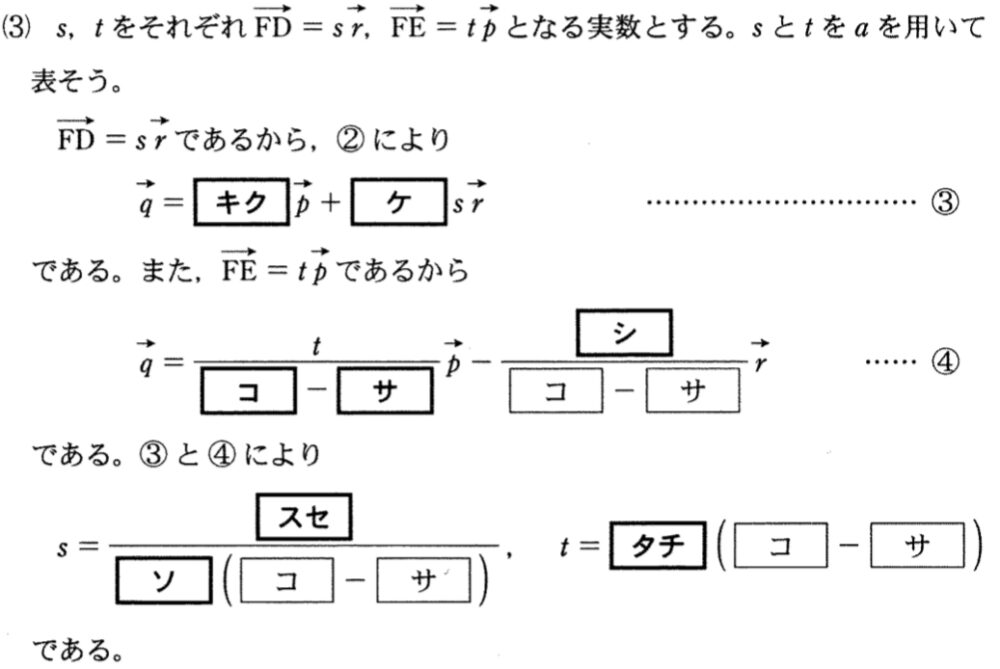
(3)解答・解説《キ〜チ》
\(\overrightarrow{FD}=s\overrightarrow{r}\) であるから,②により
\(\displaystyle\frac{3}{4}\overrightarrow{p}+\displaystyle\frac{1}{4}\overrightarrow{q}=s\overrightarrow{r}\)
よって,\(\overrightarrow{q}=-3\overrightarrow{p}+4s\overrightarrow{r}\) ・・・③《キクケ》
また,\(\overrightarrow{FE}=t\overrightarrow{p}\) であるから
\((1-a)\overrightarrow{q}+a\overrightarrow{r}=t\overrightarrow{p}\)
\(0<a<1\) より \(1-a\not=0\) であるから
よって, \(\overrightarrow{q}=\displaystyle\frac{t}{1-a}\overrightarrow{p}-\displaystyle\frac{a}{1-a}\overrightarrow{r}\) ・・・④《コサシ》
\(\overrightarrow{p}\) , \(\overrightarrow{r}\) は一次独立なベクトルであるから,③,④より
\(-3=\displaystyle\frac{t}{1-a}\) かつ \(4s=\displaystyle\frac{-a}{1-a}\)
したがって,\(s=\displaystyle\frac{-a}{4(1-a)}\) , \(t=-3(1-a)\) ・・・《ス〜チ》
(4)問題と解答・解説
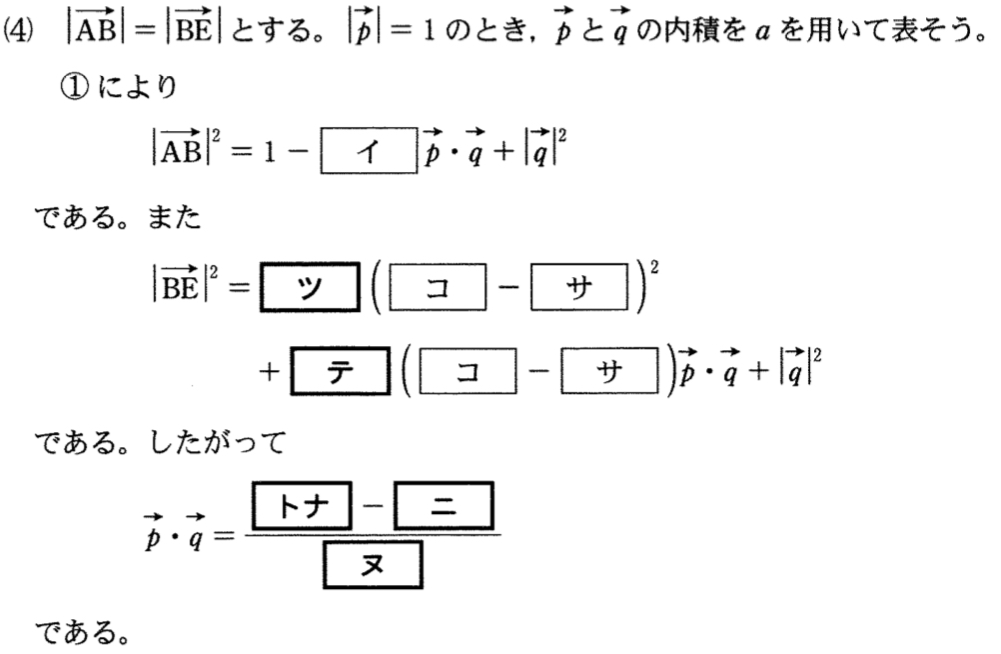
(4)解答・解説《ツ〜ヌ》
\(\left|\overrightarrow{p}\right|=1\) のとき
①より,\(\left|\overrightarrow{AB}\right|^2=1-2\overrightarrow{p}\cdot\overrightarrow{q}+\left|\overrightarrow{q}\right|^2\)
また,\(\overrightarrow{BE}=\overrightarrow{FE}-\overrightarrow{FB}=t\overrightarrow{p}-\overrightarrow{q}\)
よって,\(\overrightarrow{BE}=-3(1-a)\overrightarrow{p}-\overrightarrow{q}\) より
\(\left|\overrightarrow{BE}\right|^2=9(1-a)^2\cdot\left|\overrightarrow{p}\right|^2+6(1-a)\overrightarrow{p}\cdot\overrightarrow{q}+\left|\overrightarrow{q}\right|^2\)
\(=9(1-a)^2+6(1-a)\overrightarrow{p}\cdot\overrightarrow{q}+\left|\overrightarrow{q}\right|^2\) ・・・《ツテ》
\(\left|\overrightarrow{AB}\right|=\left|\overrightarrow{AE}\right|\) のとき
\(1-2\overrightarrow{p}\cdot\overrightarrow{q}+\left|\overrightarrow{q}\right|^2=9(1-a)^2+6(1-a)\overrightarrow{p}\cdot\overrightarrow{q}+\left|\overrightarrow{q}\right|^2\)
\(\left\{-2-6(1-a)\right\}\overrightarrow{p}\cdot\overrightarrow{q}=9(1-a)^2-1\)
\(2(3a-4)\overrightarrow{p}\cdot\overrightarrow{q}=(3a-4)(3a-2)\)
\(0<a<1\) より \(3a-4\not=0\) であるから,
\(\overrightarrow{p}\cdot\overrightarrow{q}=\displaystyle\frac{3a-2}{2}\) ・・・《ト〜ヌ》









コメント