【2023慶応義塾大学・理工・第１問】
(１) \(f(x)=x^4\) とする．\(f(x)\) の \(x=a\) における微分係数を，定義に従って求めなさい．計算過程も記述しなさい．
(２) \(g(x)=|x|\sqrt{x^2+1}\) とする．\(g(x)\) が \(x=0\) で微分可能でないことを証明しなさい．
(３) 閉区間 \([0,1]\) 上で定義された連続関数 \(h(x)\) が，開区間 \((0,1)\) で微分可能であり，この区間で常に \(h^{\prime}(x)<0\) であるとする．このとき，\(h(x)\) が区間 \([0,1]\) で減少することを，平均値の定理を用いて証明しないさい．
考え方・解答・解説
(１) 微分係数の定義
関数 \(y=f(x)\) の \(x=a\) における微分係数は
\(f^{\prime} (a)=\displaystyle\lim_{h\rightarrow 0} \displaystyle\frac{f(a+h)-f(a)}{h}\)
または \(f^{\prime} (a)=\displaystyle\lim_{b\rightarrow a} \displaystyle\frac{f(b)-f(a)}{b-a}\)
(１) 解答・解説
\(f^{\prime}(a)=\displaystyle\lim_{h\rightarrow 0}\displaystyle\frac{f(a+h)-f(a)}{h}\)
\(=\displaystyle\lim_{h\rightarrow 0}\displaystyle\frac{(a+h)^4-a^4}{h}\)
\(=\displaystyle\lim_{h\rightarrow 0}\displaystyle\frac{(a^4+4a^3h+6a^2h^2+4ah^3+h^4)-a^4}{h}\)
\(=\displaystyle\lim_{h\rightarrow 0}(4a^3+6a^2h+4ah^2+h^3) \)
\(=4a^3\)
(２) 関数の微分可能性
ある関数 \(f(x)\) において，微分係数
\(f^{\prime}(a)=\displaystyle\lim_{h\rightarrow 0}\displaystyle\frac{f(a+h)-f(a)}{h}=\displaystyle\lim_{x\rightarrow a}\displaystyle\frac{f(x)-f(a)}{x-a}\)
が存在するとき，
\(f(x)\) は \(x=a\) において微分可能である
(２) 解答・解説
\(x>0\) のとき \(g(x)=x\sqrt{x^2+1}\) より
\(\displaystyle\lim_{h\rightarrow +0}\displaystyle\frac{g(0+h)-g(0)}{h}=\displaystyle\lim_{h\rightarrow +0}\displaystyle\frac{h\sqrt{h^2+1}-0}{h}\)
\(=\displaystyle\lim_{h\rightarrow +0}\sqrt{h^2+1}=1\)
\(x<0\) のとき \(g(x)=-x\sqrt{x^2+1}\) より
\(\displaystyle\lim_{h\rightarrow -0}\displaystyle\frac{g(0+h)-g(0)}{h}=\displaystyle\lim_{h\rightarrow -0}\displaystyle\frac{-h\sqrt{h^2+1}-0}{h}\)
\(=\displaystyle\lim_{h\rightarrow -0}\left(-\sqrt{h^2+1}\right)=-1\)
よって\(g^{\prime}(0)\) は存在しないため，\(g(x)\) は \(x=0\) で微分可能でない．
(３) 平均値の定理
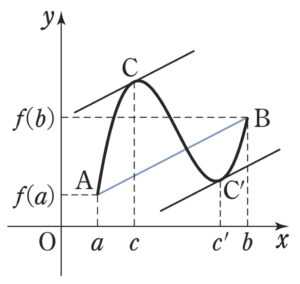関数 \(f(x)\) が閉区間 \([a,b]\) で連続で，
開区間 \((a,b)\) で微分可能ならば，
\(\displaystyle\frac{f(b)-f(a)}{b-a}=f^{\prime}(c)\) ， \(a<c<b\)
を満たす実数 \(c\) が存在する．
(３) 解答・解説
平均値の定理より，\(0≦a<b≦1\) を満たす任意の実数 \(a\) , \(b\) に対して
\(\displaystyle\frac{h(b)-h(a)}{b-a}=h^{\prime}(c)\)
を満たす実数 \(c\) が \(a<c<b\) に存在する．
\(h^{\prime}(c)<0\) のとき
\(\displaystyle\frac{h(b)-h(a)}{b-a}<0\)
\(a<b\) より \(b-a>0\) なので
\(h(b)-h(a)<0\)
よって，\(h(b)<h(a)\)
したがって，\(h(x)\) は区間 \([0,1]\) で減少する．
コメント