【2023数学ⅠA(第1日程)】第２問[１](データの分析)

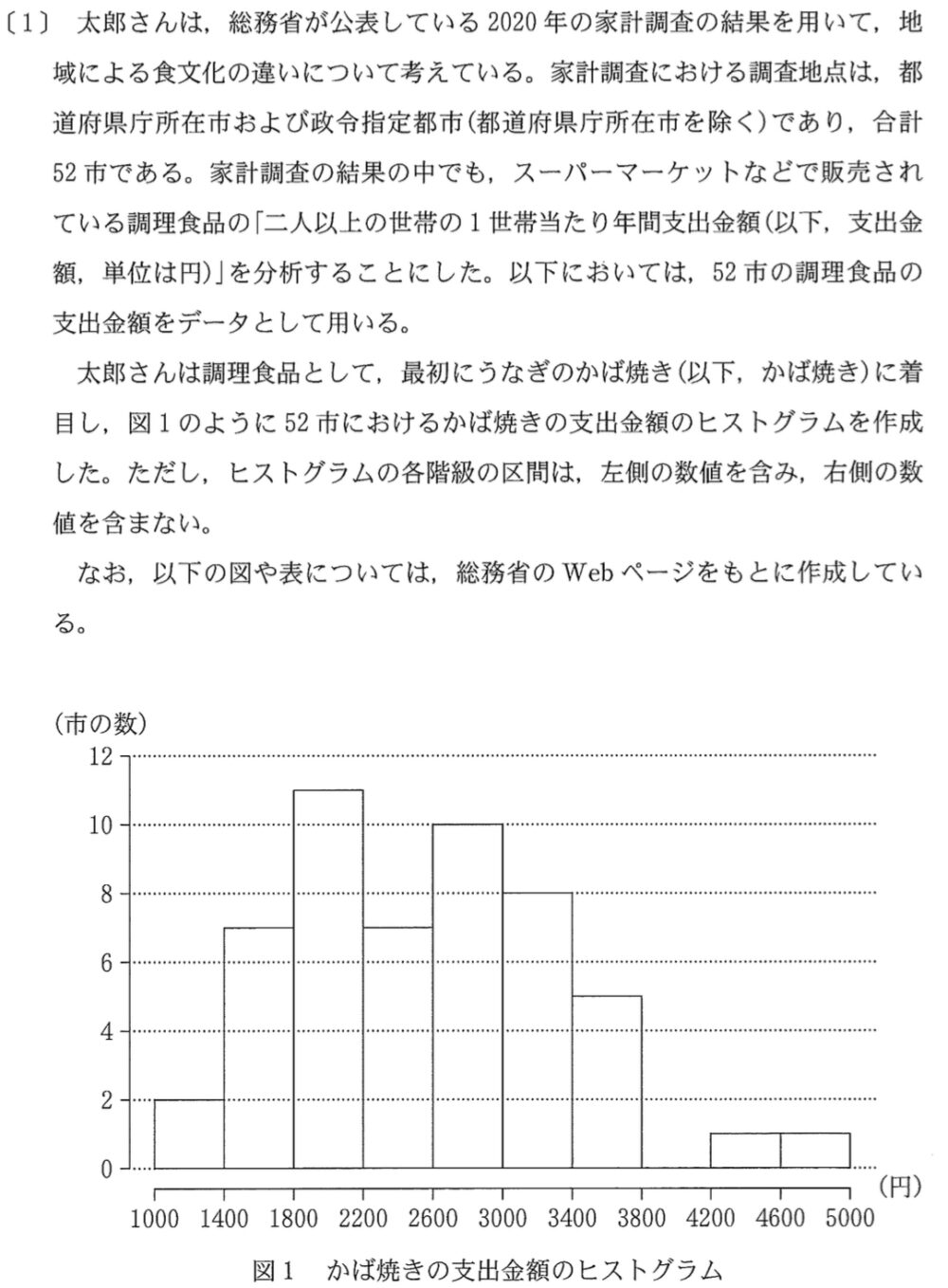
(１)問題と解答・解説《ア〜ウ》

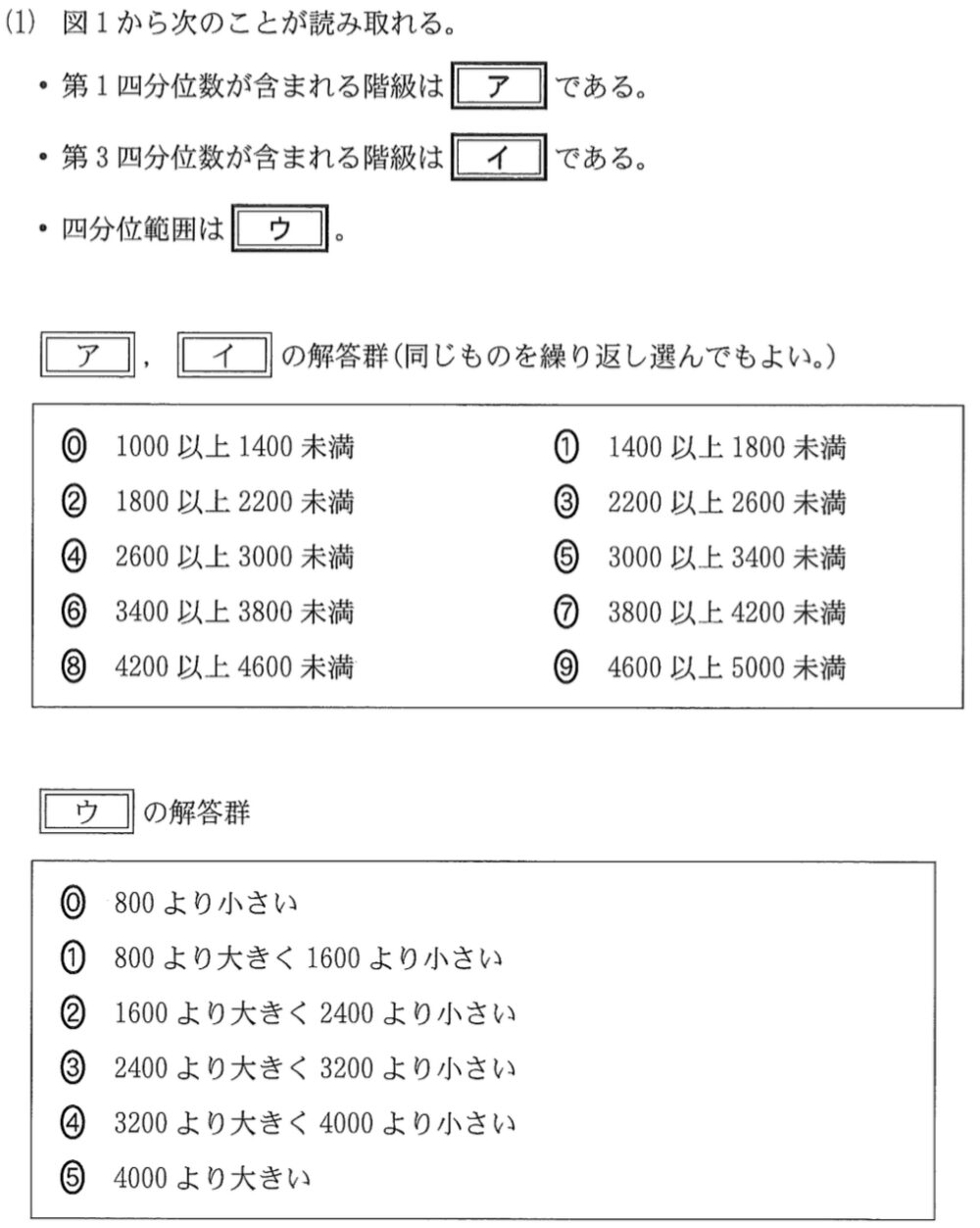
(１)解答・解説《ア〜ウ》

$52$ 市におけるデータの第 $1$ 四分位数は，$13$ 番目と $14$ 番目の平均をとった値となるので，

ヒストグラムから，第 $1$ 四分位数が含まれる階級は $1800$ 以上 $2200$ 未満・・・《ア：②》

$52$ 市におけるデータの第 $3$ 四分位数は，$39$ 番目と $40$ 番目の平均をとった値となるので，

ヒストグラムから，第 $3$ 四分位数が含まれる階級は $3000$ 以上 $3400$ 未満・・・《イ：⑤》

第 $1$ 四分位数を $Q_{1}$，第 $3$ 四分位数を $Q_{3}$ とおくと

$1800≦Q_{1}<2200$，$3000≦Q_{3}<3400$ より

四分位範囲 $Q_{3}-Q_{1}$ は

$3000-2200<Q_{3}-Q_{1}<3400-1800$

よって，$800<Q_{3}-Q_{1}<1600$ ・・・《ウ：①》

(２)(ⅰ)問題と解答・解説《エ》

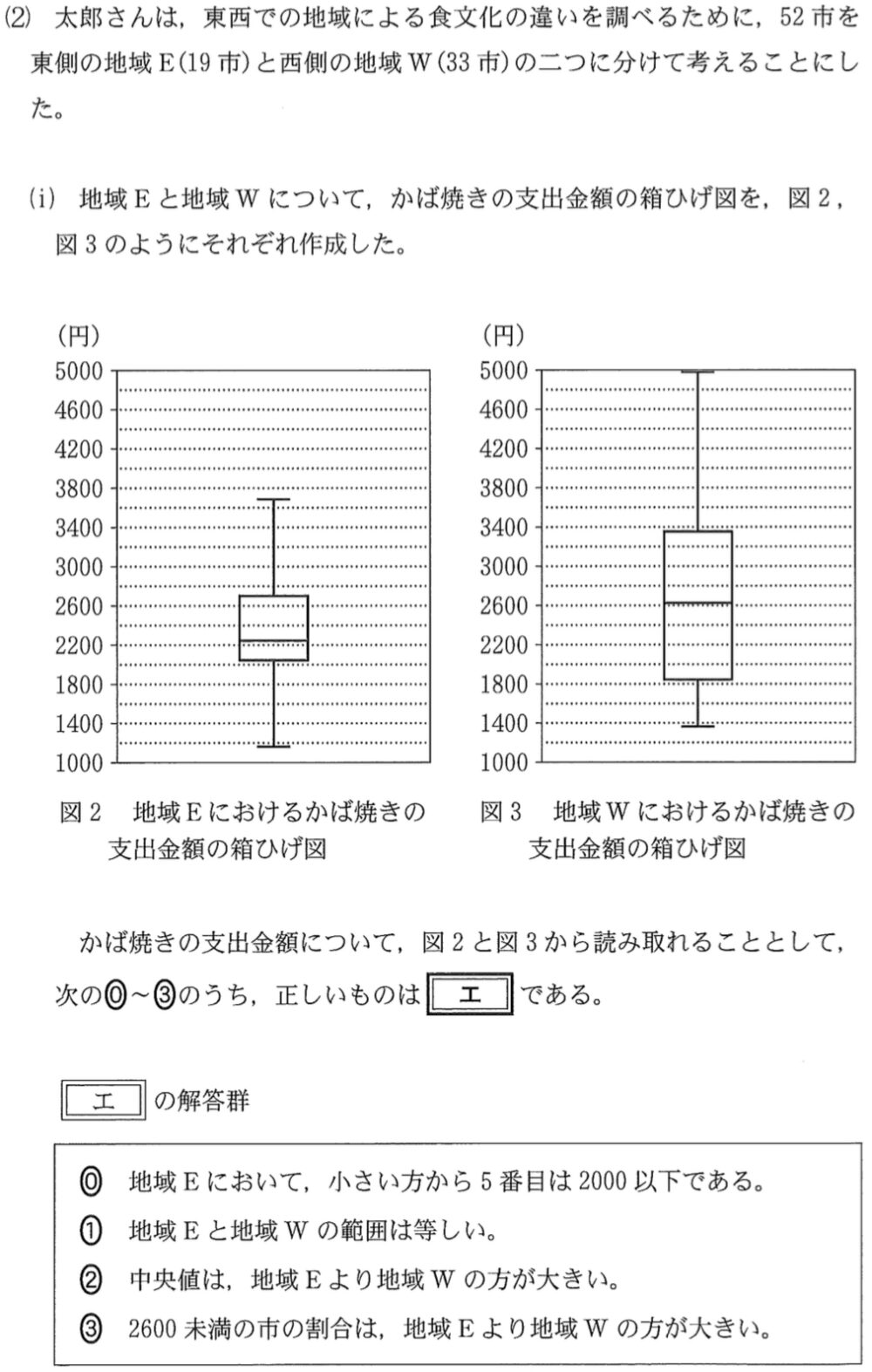
(２)(ⅰ)解答・解説《エ》

⓪について

地域 $E$ は $19$ 市より

第 $1$ 四分位数は小さい方から数えて $5$ 番目の値となる．

図 $2$ の箱ひげ図から，第 $1$ 四分位数は $2000$ より大きく $2200$ 未満であるので，

⓪は正しくない．

①について

地域 $E$ の最大値は $3600〜3800$，最小値は $1000〜1200$ より

範囲は $2400〜2800$ となる．

地域 $W$ の最大値は $4800〜5000$，最小値は $1200〜1400$ より

範囲は $3400〜3800$ となる．

よって地域 $E$ の範囲の方が小さいため，①は正しくない．

②について

地域 $E$ の中央値は $2200〜2400$，地域 $W$ の中央値は $2600〜2800$

よって中央値は，地域 $E$ より地域 $W$ の方が大きいため，②は正しい．

③について

それぞれの中央値に注目すると，

地域 $E$ は $2600$ 未満の割合は $5$ 割を超えるが，

地域 $W$ は $2600$ 未満の割合は $5$ 割未満となる．

よって，$2600$ 未満の市の割合は，地域 $E$ より地域 $W$ の方が小さいため

③は正しくない．

以上から，正しいものは《エ：③》

(２)(ⅱ)問題と解答・解説《オ》分散について

(２)(ⅱ)解答・解説《オ》分散について

分散の定義から

地域 $E$ におけるかば焼きの支出金額の分散は，地域 $E$ のそれぞれの市におけるかば焼きの支出金額の偏差の《オ：② $2$ 乗を合計して地域 $E$ の市の数で割った値》である．

(３)問題と解答・解説《カ》相関係数

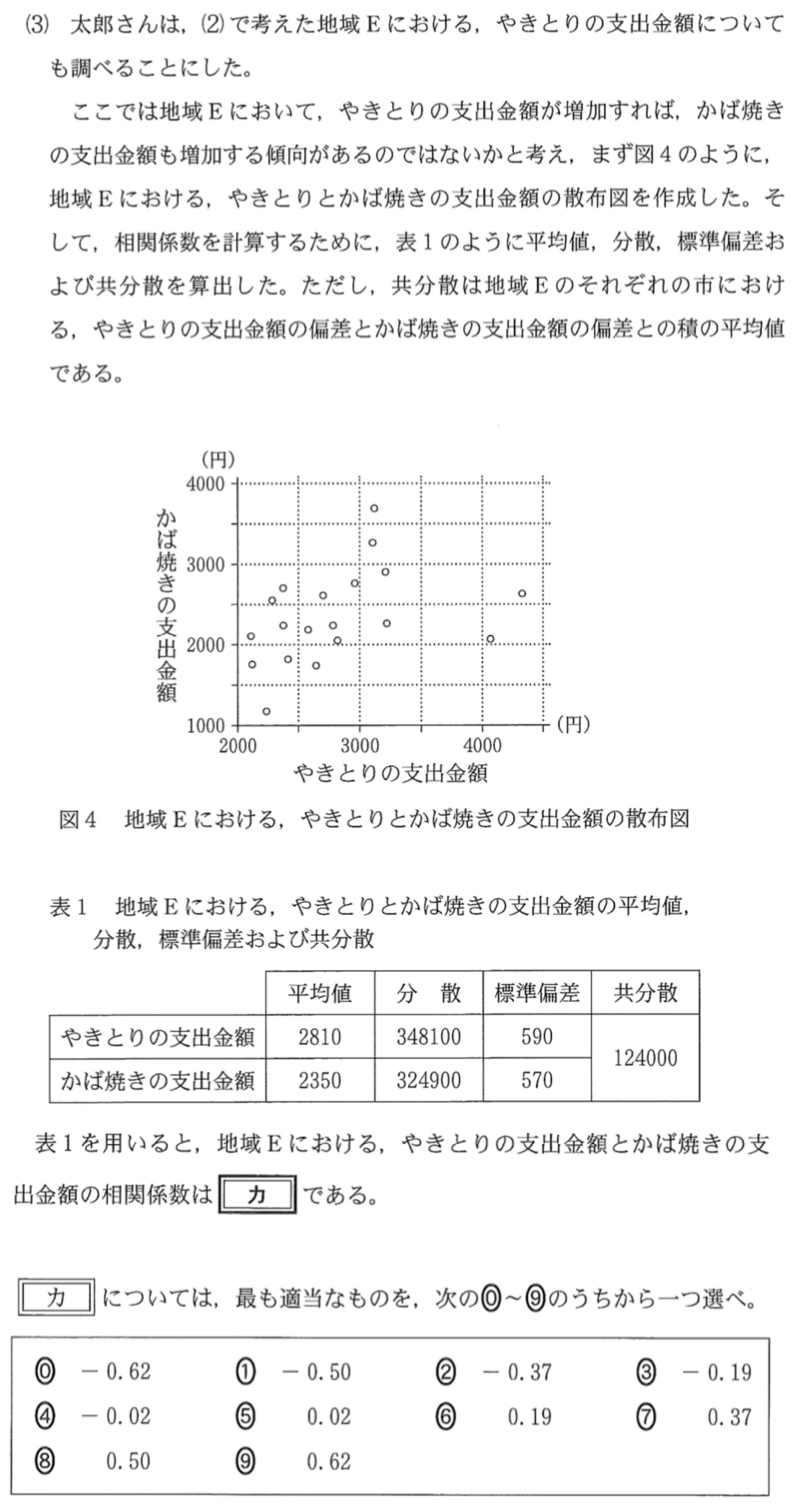
(３)解答・解説《カ》相関係数

$r=\displaystyle\frac{124000}{590\times 570}=0.368\cdots$

よって，《カ：⑦》