【2023数学ⅡB(第1日程)】第１問[１](三角関数)

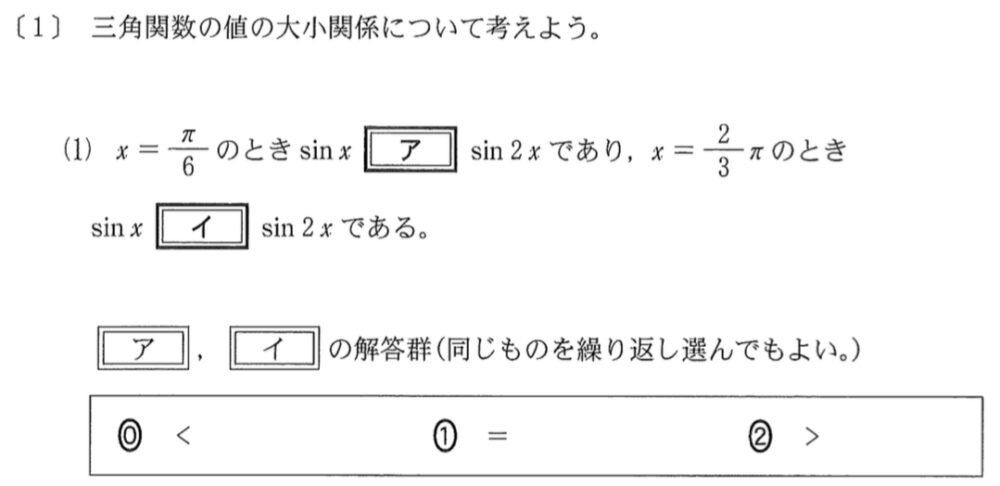
(１)問題と解答・解説《アイ》

(１)解答・解説《アイ》

\(x=\displaystyle\frac{\pi}{6}\) のとき

\(\sin x=\sin \displaystyle\frac{\pi}{6}=\displaystyle\frac{1}{2}\)

\(\sin 2x=\sin \displaystyle\frac{\pi}{3}=\displaystyle\frac{\sqrt{3}}{2}\) より

\(\sin x<\sin 2x\) ・・・《ア：⓪》

\(x=\displaystyle\frac{2\pi}{3}\) のとき

\(\sin x=\sin \displaystyle\frac{2\pi}{3}=\displaystyle\frac{\sqrt{3}}{2}\)

\(\sin 2x=\sin \displaystyle\frac{4\pi}{3}=-\displaystyle\frac{\sqrt{3}}{2}\) より

\(\sin x>\sin 2x\) ・・・《イ：②》

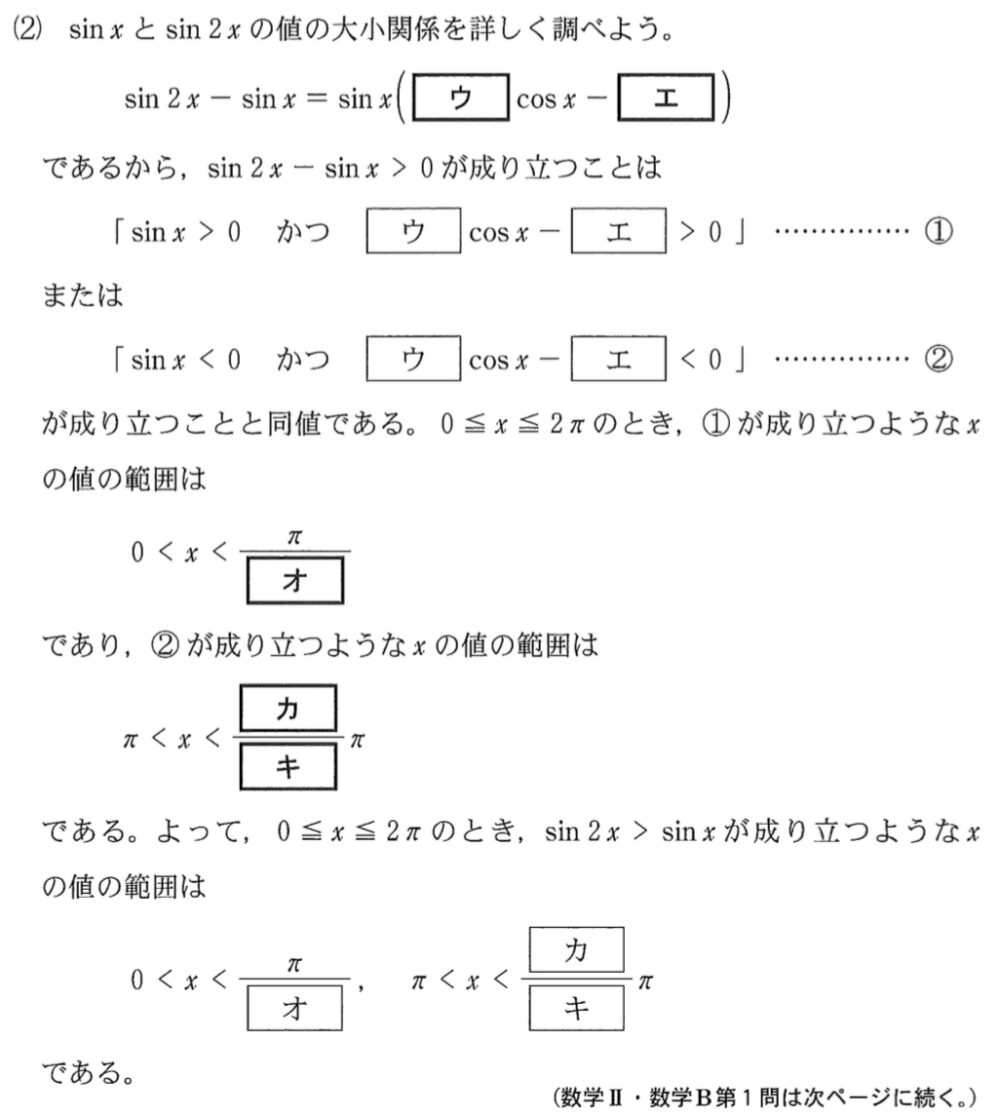
(２)問題と解答・解説《ウ〜キ》

(２)解答・解説《ウ〜キ》

\(\sin 2x-\sin x=2\sin x\cos x-\sin x\)

\(=\)\(\sin x(2\cos x-1)\) ・・・《ウエ》

\(\sin 2x-\sin x>0\) が成り立つことは，

「\(\sin x>0\) かつ \(2\cos x-1>0\)」・・・①

または

「\(\sin x<0\) かつ \(2\cos x-1<0\)」・・・②

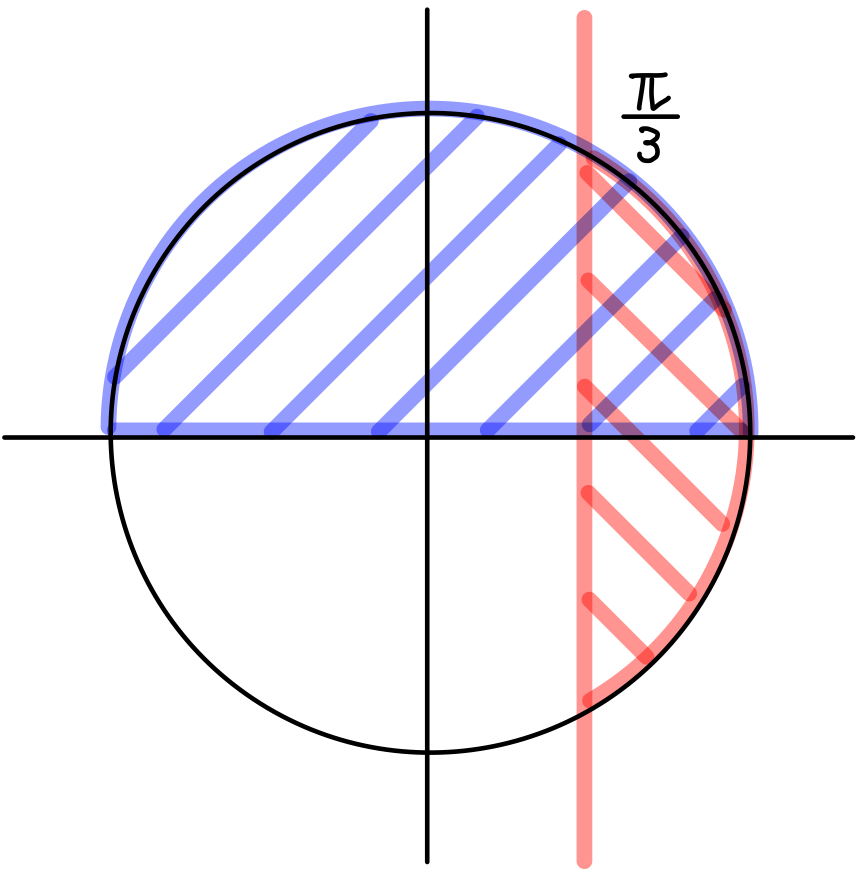①のとき

\(\sin x>0\) かつ \(\cos x>\displaystyle\frac{1}{2}\)

\(0≦x<2\pi\) より，\(0<x<\displaystyle\frac{\pi}{3}\) ・・・《オ》

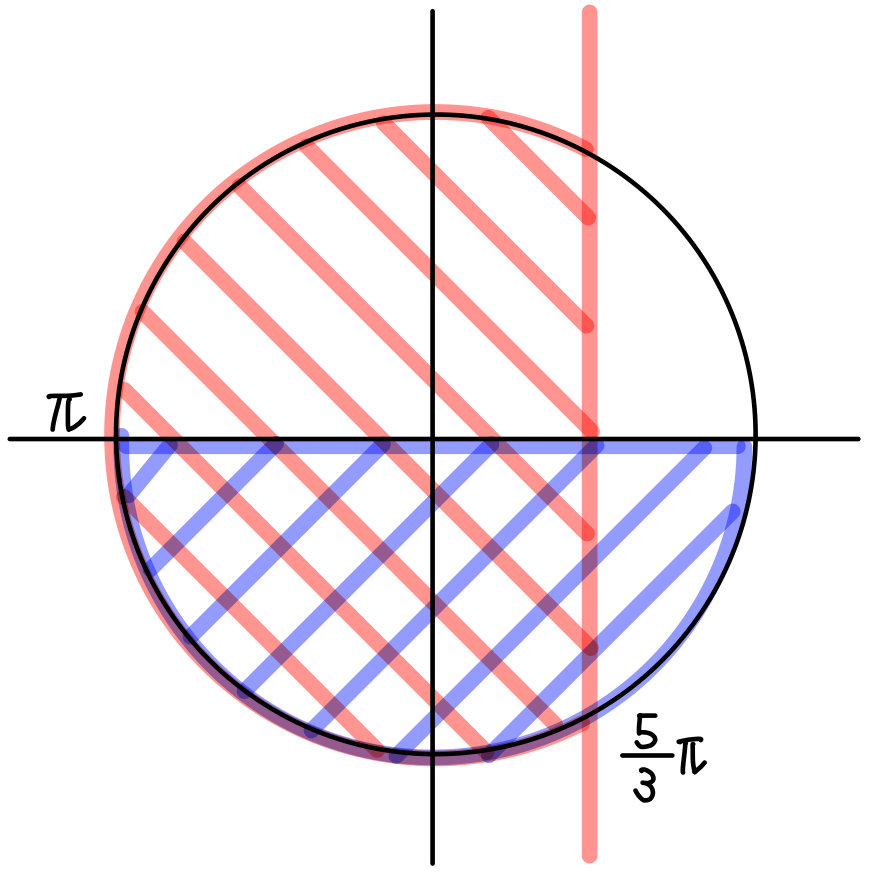②のとき

\(\sin x<0\) かつ \(\cos x<\displaystyle\frac{1}{2}\)

\(0≦x<2\pi\) より，\(\pi<x<\displaystyle\frac{5\pi}{3}\) ・・・《カキ》

(３)問題と解答・解説《ク〜セ》

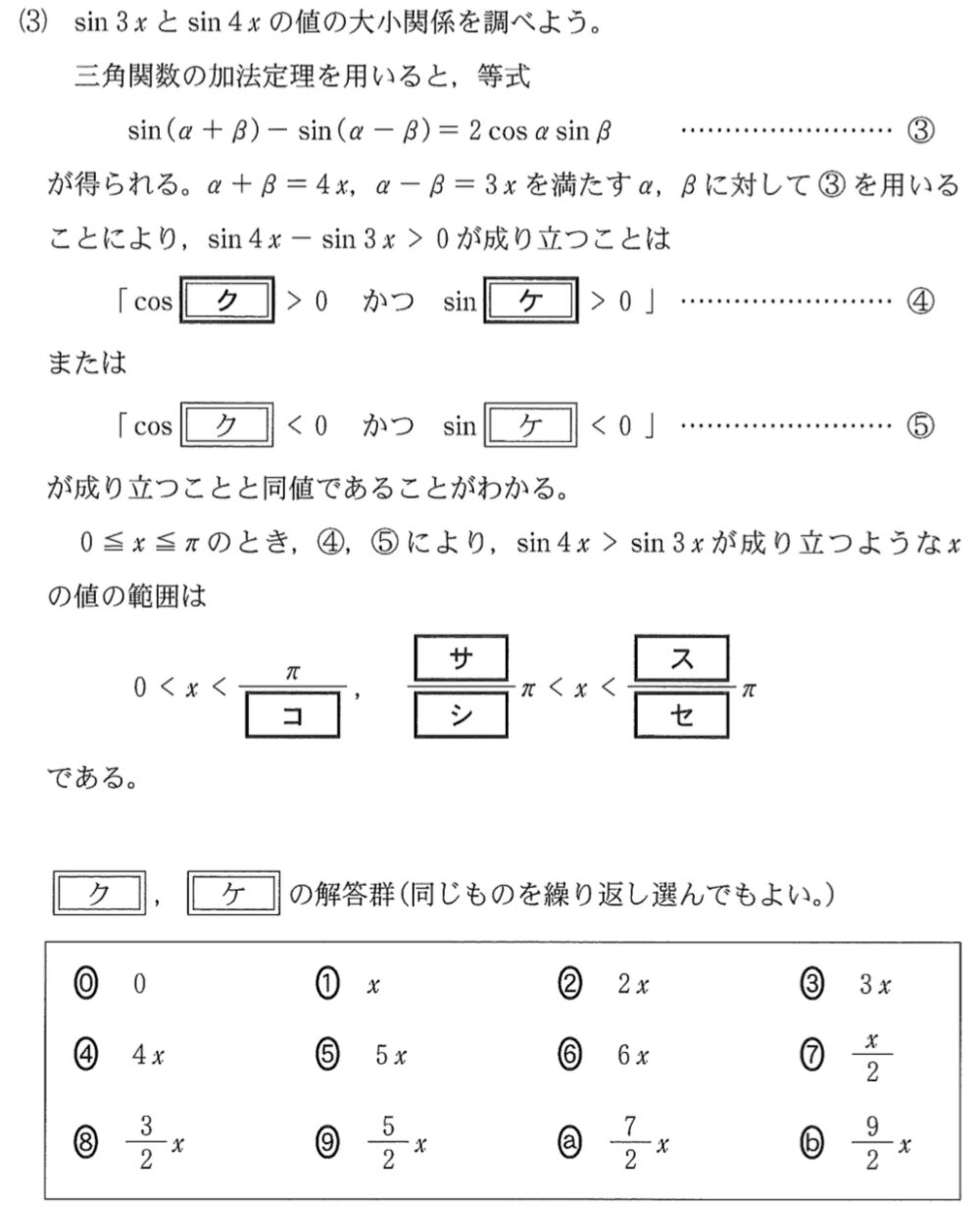
(３)解答・解説《ク〜セ》

\(\sin 3x\) と \(\sin 4x\) の値の大小関係について

三角関数の加法定理を用いると

\(\sin(\alpha+\beta)-\sin(\alpha-\beta)=2\cos\alpha\sin\beta\) ・・・③

\(\begin{cases}\alpha+\beta=4x\\\alpha-\beta=3x \end{cases}\)

\(\iff\) \(\alpha=\displaystyle\frac{7x}{2}\) ，\(\beta=\displaystyle\frac{x}{2}\) より

③から

\(\sin 4x-\sin 3x=2\cos\displaystyle\frac{7x}{2}\sin\displaystyle\frac{x}{2}\)

\(\sin 4x-\sin 3x>0\) が成り立つことは

「\(\cos\displaystyle\frac{7x}{2}>0\) かつ \(\sin\displaystyle\frac{x}{2}>0\)」・・・④

または

「\(\cos\displaystyle\frac{7x}{2}<0\) かつ \(\sin\displaystyle\frac{x}{2}<0\)」・・・⑤

よって，《ク：\(a\) ，ケ：⑦》

ここで，\(0≦x≦\pi\) のとき

\(0≦\displaystyle\frac{x}{2}≦\displaystyle\frac{\pi}{2}\) より \(\sin \displaystyle\frac{x}{2}≧0\)

よって⑤は成立しない．

④のとき \(0≦x≦\pi\) より \(0≦\displaystyle\frac{7x}{2}≦\displaystyle\frac{7\pi}{2}\) のとき

\(\cos\displaystyle\frac{7x}{2}>0\)

\(\iff\) \(0<\displaystyle\frac{7x}{2}<\displaystyle\frac{\pi}{2}\)，\(\displaystyle\frac{3\pi}{2}<\displaystyle\frac{7x}{2}<\displaystyle\frac{5\pi}{2}\)

\(\iff\) \(0<x<\displaystyle\frac{\pi}{7}\)，\(\displaystyle\frac{3\pi}{7}<x<\displaystyle\frac{5\pi}{7}\) ・・・⑥

⑥のとき \(\sin\displaystyle\frac{x}{2}>0\) は常に満たすので，

したがって求める範囲は，

\(0<x<\displaystyle\frac{\pi}{7}\)，\(\displaystyle\frac{3\pi}{7}<x<\displaystyle\frac{5\pi}{7}\) ・・・《コ〜セ》

(４)問題と解答・解説《ソ〜チ》

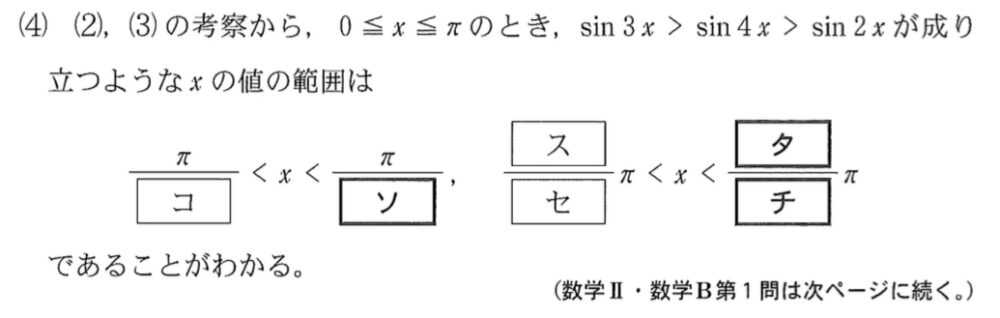
(４)解答・解説《ソ〜チ》

\(\sin 3x>\sin 4x>\sin 2x\)

\(\iff\) \(\begin{cases}\sin 3x>\sin 4x\\\sin 4x>\sin 2x\end{cases}\)

・\(\sin 3x>\sin 4x\) のとき

(３)の結果を利用すると

\(\displaystyle\frac{\pi}{7}<x<\displaystyle\frac{3\pi}{7}\)，\(\displaystyle\frac{5\pi}{7}<x≦\pi\) ・・・⑦

・\(\sin 4x>\sin 2x\) のとき

(２)の結果において \(x\) を \(2x\) と置き換えればよいので

\(0<2x<\displaystyle\frac{\pi}{3}\) ，\(\pi<2x<\displaystyle\frac{5\pi}{3}\)

\(\iff\) \(0<x<\displaystyle\frac{\pi}{6}\) ，\(\displaystyle\frac{\pi}{2}<x<\displaystyle\frac{5\pi}{6}\) ・・・⑧

⑦，⑧より

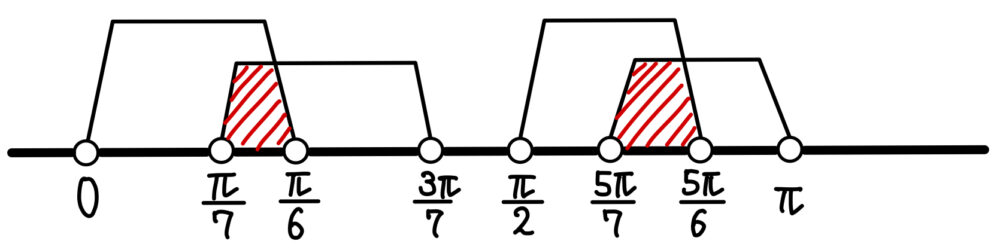
\(\displaystyle\frac{\pi}{7}<x<\displaystyle\frac{\pi}{6}\)，\(\displaystyle\frac{5\pi}{7}<x<\displaystyle\frac{5\pi}{6}\) ・・・《ソ〜チ》