(１)問題《コ～タ》
(１)解答・解説《コ～タ》
\(P(x)=2x^3+7x^2+10x+5\)，\(S(x)=x^2+4x+7\) について
\(S(x)=0\) \(\iff\) \(x^2+4x+7=0\)
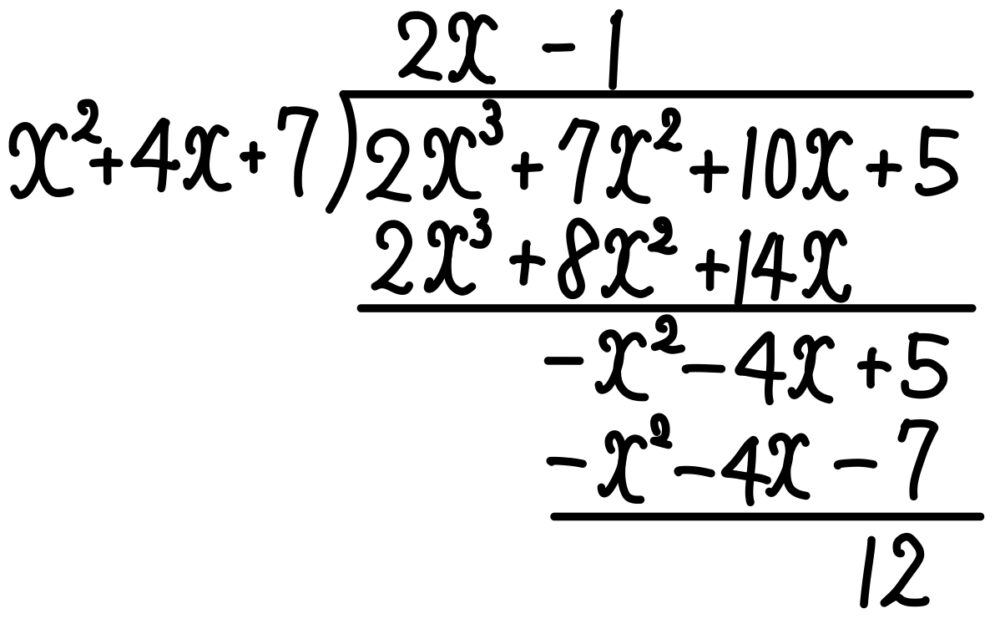これを解くと，\(x=-2\pm\sqrt{3}i\) ・・・《コ～シ》
また，\(P(x)\) を \(S(x)\) で割ると
商 \(T(x)=2x-1\) ，余り \(U(x)=12\) ・・・《ス～タ》
(２)(ⅰ)問題《チツ》
(２)(ⅰ)解答・解説《チツ》
\(S(x)=0\) が異なる \(2\) 解 \(\alpha\)，\(\beta\) をもっているので
\(S(\alpha)=S(\beta)=0\) ・・・①
また \(P(x)\) を \(S(x)\) で割った余りが定数 ( \(U(x)=k\) ) となるので
\(P(x)=S(x)T(x)+k\) ・・・②
②に \(x=\alpha\) ，\(\beta\) をそれぞれ代入すると
\(P(\alpha)=S(\alpha)T(\alpha)+k\)，\(P(\beta)=S(\beta)T(\beta)+k\)
①より \(P(\alpha)=P(\beta)=k\) となることが導かれる．
したがって，余りが定数になるとき，\(P(\alpha)=P(\beta)\) が成り立つ．
《チ：③，ツ：①》
(２)(ⅱ)問題《テ～ナ》
(２)(ⅱ)解答・解説《テ～ナ》
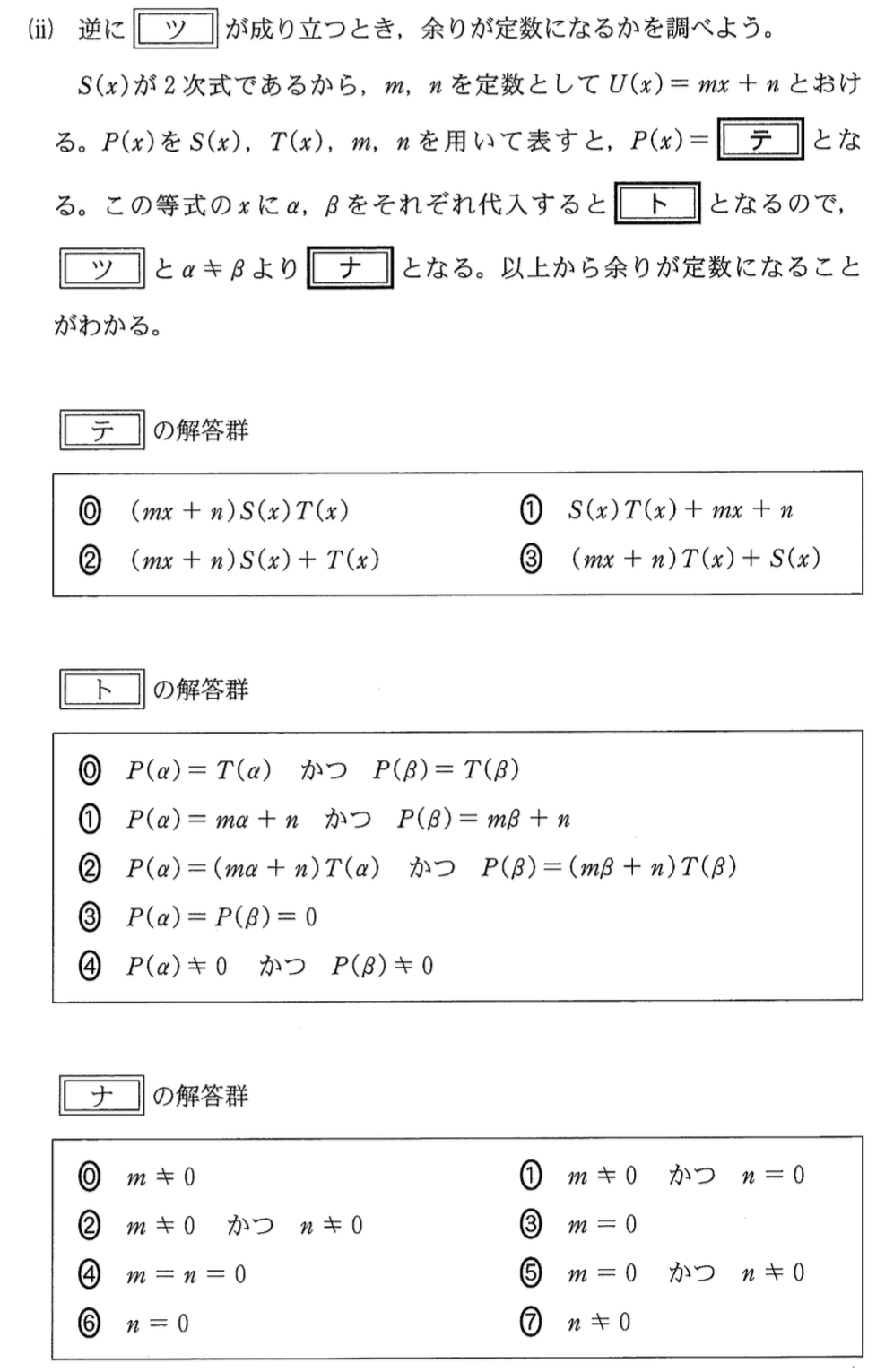
逆に \(P(\alpha)=P(\beta)\) が成り立つとき
\(S(x)\) が \(2\) 次式であるから，\(m\)，\(n\) を定数として \(U(x)=mx+n\) とおけるので，
\(P(x)=S(x)T(x)+mx+n\) ・・・《テ：①》
この等式に \(x=\alpha\)，\(\beta\) をそれぞれ代入すると \(S(\alpha)=S(\beta)=0\) なので
\(P(\alpha)=m\alpha+n\)，\(P(\alpha)=m\beta+n\) ・・・《ト：①》
\(P(\alpha)=P(\beta)\) より
\(m\alpha+n=m\beta+n\) \(\iff\) \(m(\alpha-\beta)=0\)
\(\alpha\not=\beta\) より，\(m=0\) ・・・《ナ：③》
以上から余りが定数になることがわかる．
(３)問題《ニ～ノ》
(３)解答・解説《ニ～ノ》
\(P(x)=x^{10}-2x^9-px^2-5x\) ，\(S(x)=x^2-x-2\) の場合を考える．
\(P(x)\) を \(S(x)\) で割った余りが定数になるとき，
(２)の結果から \(P(\alpha)=P(\beta)\)
\(S(x)=0\) を解くと
\(x^2-x-2=0\)
\((x+1)(x-2)=0\)
\(x=-1,2\) (\(\alpha=-1,\beta=2\) と考え)
\(P(-1)=P(2)\)
\(1+2-p+5=1024-1024-4p-10\)
よって \(p=-6\) ・・・《ニヌ》となり，
その余りは \(P(-1)=P(2)=\)\(14\) ・・・《ネノ》
コメント