【お茶の水女子大学】
\(n\) を自然数とする.不等式
\(y≦2n^2\) , \(y≧\displaystyle\frac{1}{2}x^2\) , \(x≧0\)
を同時に満たす整数の組 \((x,y)\) の個数を求めよ.
格子点問題の考え方
格子点
⇒ \(x\) or \(y\) 軸に平行な直線ごとにカウントし,総和(Σ)を考える


解答・解説
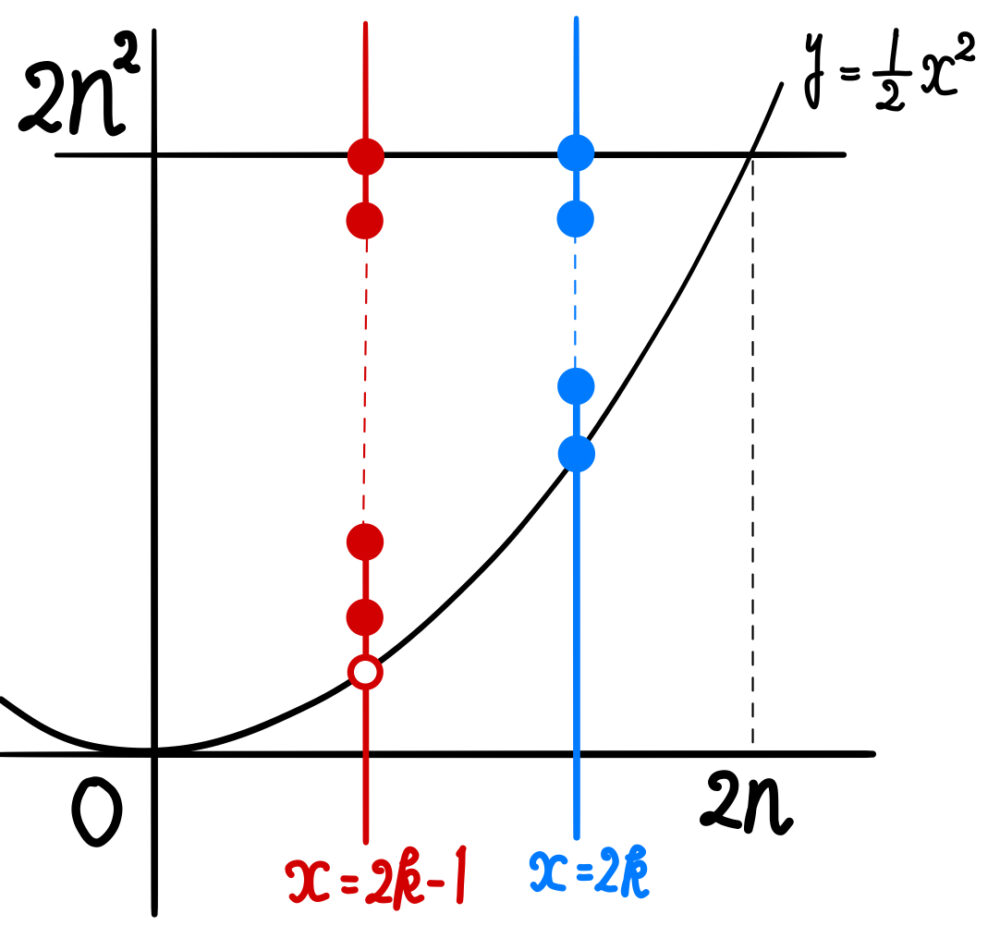
( ⅰ ) \(x=2k\) ( \(0≦k≦n\) ) 上には
\((2k,2k^2)\) , \((2k,2k^2+1)\) , \((2k,2k^2+2)\) , \(\cdots\) , \((2k,2n^2)\) の
\(2n^2-2k^2+1\) 個の格子点がある.
( ⅱ ) \(x=2k-1\) ( \(0≦k≦n\) ) 上には

\(x=2k-1\) を \(y=\displaystyle\frac{1}{2}x^2\) に代入すると
\(y=\displaystyle\frac{1}{2}(2k-1)^2=2k^2-2k+\displaystyle\frac{1}{2}\)
これは格子点ではないため,領域に含まれる格子点は \(y\) 軸方向に \(\displaystyle\frac{1}{2}\) だけ上にある,\((2k-1,2k^2-2k+1)\) が格子点となる!
\((2k-1,2k^2-2k+1)\) , \((2k-1,2k^2-2k+2)\) , \(\cdots\) , \((2k,2n^2)\) の
\(2n^2-(2k^2-2k+1)+1=2n^2-2k^2+2k\) 個の格子点がある.
よって求める格子点の個数は
\(\displaystyle\sum_{k=0}^{n}{(2n^2-2k^2+1)}+\displaystyle\sum_{k=1}^{n}{(2n^2-2k^2+2k)}\)
\(=2n^2+1+\displaystyle\sum_{k=1}^{n}{(2n^2-2k^2+1)}+\displaystyle\sum_{k=1}^{n}{(2n^2-2k^2+2k)}\)
\(=2n^2+1+\displaystyle\sum_{k=1}^{n}{(-4k^2+2k+4n^2+1)}\)
\(=2n^2+1-\displaystyle\frac{4}{6}n(n+1)(2n+1)+\displaystyle\frac{2}{2}n(n+1)+n(4n^2+1)\)
\(=\displaystyle\frac{1}{3}(8n^3+3n^2+4n+3)\)








コメント