【2021数学ⅠA(第２日程)】第５問(図形の性質)

(１)問題と解答・解説《ア〜キ》

(１)解答・解説《ア〜キ》

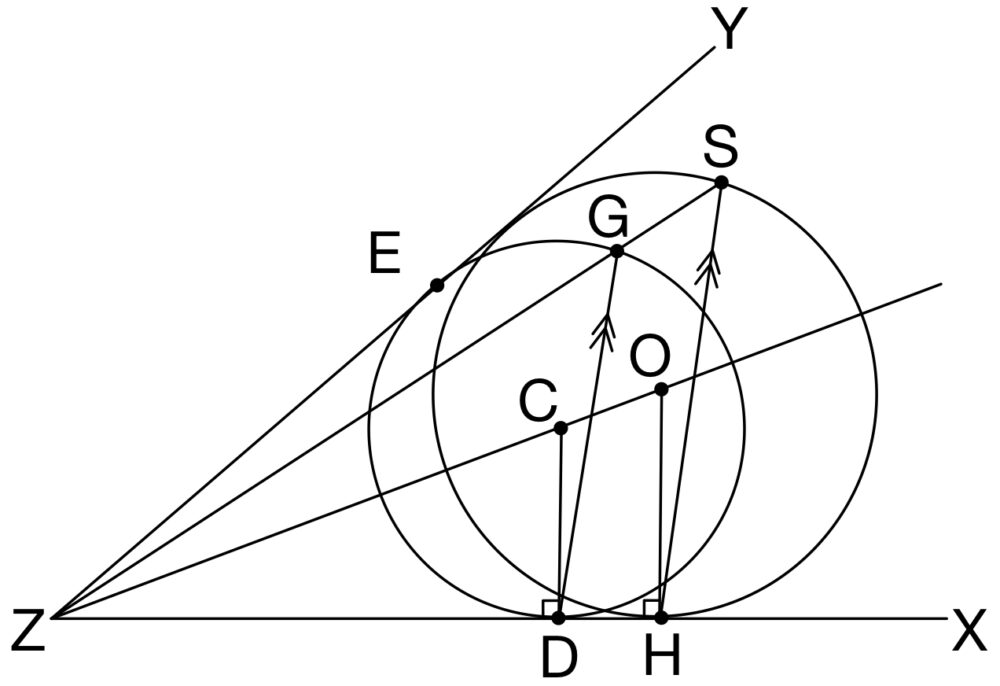円 $O$ が点 $S$ を通り，半直線 $ZX$ と半直線 $ZY$ の両方に接する円であることを示すには，$OH=OS$ ・・・《ア：⑤》が成り立つことを示せば良い．

$\triangle ZDG$ と $\triangle ZHS$ との関係は，

$\angle DZG=\angle HZS$ (共通角)，$\angle ZDG=\angle ZHS$ (同位角) であるから，相似である．

また，$\triangle ZDC$ と $\triangle ZHO$ との関係は，

$\angle DZC=\angle HZO$ (共通角)，$\angle ZDC=\angle ZHO=90°$ であるから，相似である．

よって，

$DG:HS=ZD:ZH$ ・・・《イ：②，ウ：⑥，エ：⑦》

$DC:HO=ZD:ZH$ ・・・《オ：①》

であるから，$DG:HS=DC:HO$ となる．

ここで，$3$ 点 $S$，$O$，$H$ が一直線上にない場合は，

$\angle CDG=\angle ZDG-90°=\angle ZHS-90°=\angle OHS$ ・・・《カ：②》より

$\triangle CDG\text{∽}\triangle OHS$

よって，$CD=CG$ より，$OH=OS$ であることが分かる．

なお，$3$ 点 $S$，$O$，$H$ が一直線上にある場合，$DG / / HS$ であるから，$3$ 点 $G$，$C$，$D$ は一直線上にある．

よって，$DG=2DC$ ・・・《キ》

となり，$DG:HS=DC:HO$ より，$OH=OS$ である．

(２)問題と解答・解説《ク〜テ》

(２)解答・解説《ク〜テ》

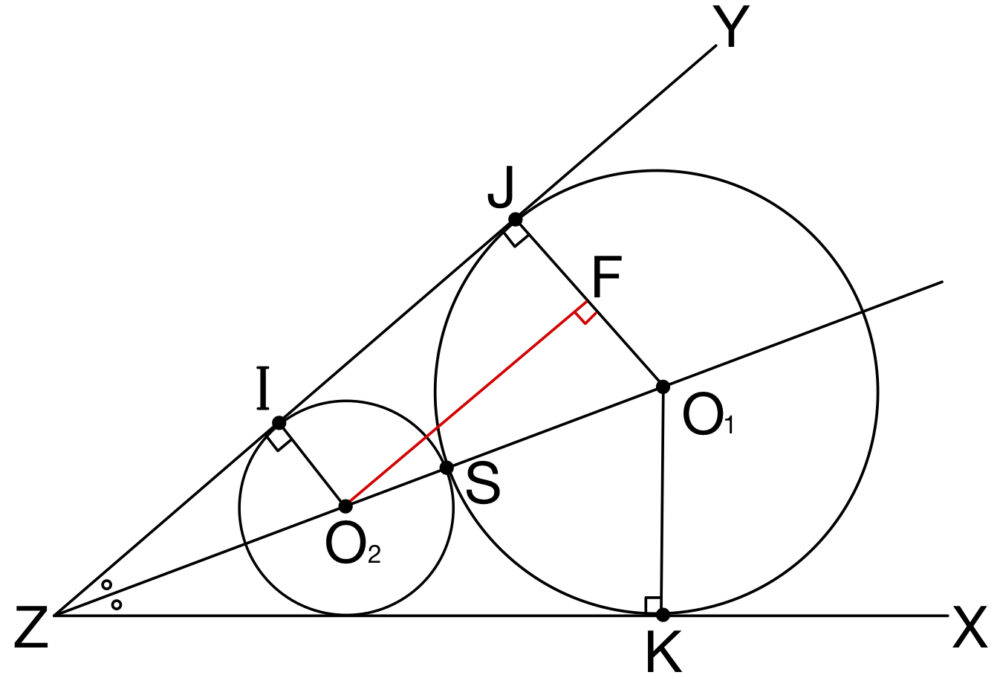
点 $O_{2}$ から線分 $O_{1}J$ に垂線 $O_{2}F$ を引くと，

図より，$IJ=O_{2}F$ であるから

直角三角形 $O_{1}O_{2}F$ で三平方の定理から

$IJ=O_{2}F=\sqrt{O_{1}O_{2}^2-O_{1}F^2}$

$=\sqrt{(5+3)^2-(5-3)^2}=$$2\sqrt{15}$  ・・・《ク〜コ》

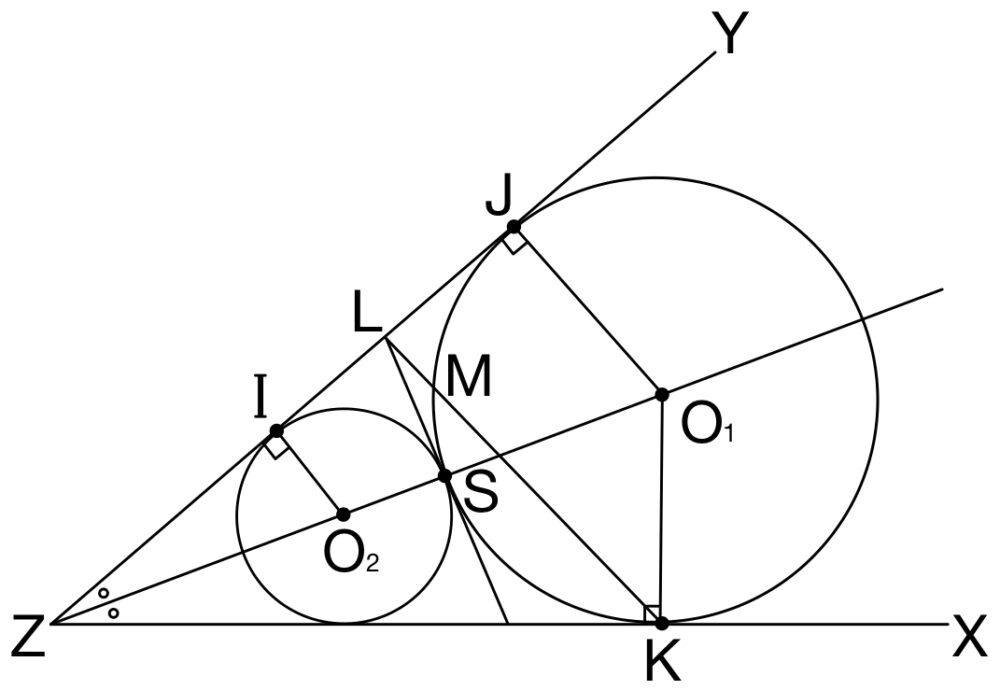
円 $O_{1}$ において方べきの定理から

$LM\cdot LK=LJ^2$ ・・・① が成り立つ．

また，直線 $LJ$ と直線 $LS$ は円 $O_{1}$ の接線であるから，

$LJ=LS$ ・・・②

直線 $LI$ と直線 $LS$ は円 $O_{2}$ の接線であるから，

$LI=LS$ ・・・③

②，③より $LJ=LI$

よって $L$ は線分 $IJ$ の中点となるので，$LJ=\displaystyle\frac{1}{2}IJ=\displaystyle\frac{1}{2}\cdot 2\sqrt{15}=\sqrt{15}$ であるから，

①より，$LM\cdot LK=\left(\sqrt{15}\right)^2=$$15$  ・・・《サシ》

また，$\triangle ZIO_{2}\text{∽}\triangle ZJO_{1}$ より

$ZI:ZJ=IO_{2}:JO_{1}$

$ZI:(ZI+IJ)=3:5$

$ZI:(ZI+2\sqrt{15})=3:5$

よって，$ZI=3\sqrt{15}$ ・・・《ス〜ソ》

線分 $ZN$ は $\angle LZK$ の二等分線より，

$LN:NK=ZL:ZK$ であるから，

$LN:NK=(ZI+IL):ZJ$

$LN:NK=(3\sqrt{15}+\sqrt{15}):(3\sqrt{15}+2\sqrt{15})$

であるから，$\displaystyle\frac{LN}{NK}=\displaystyle\frac{4}{5}$ ・・・《タチ》

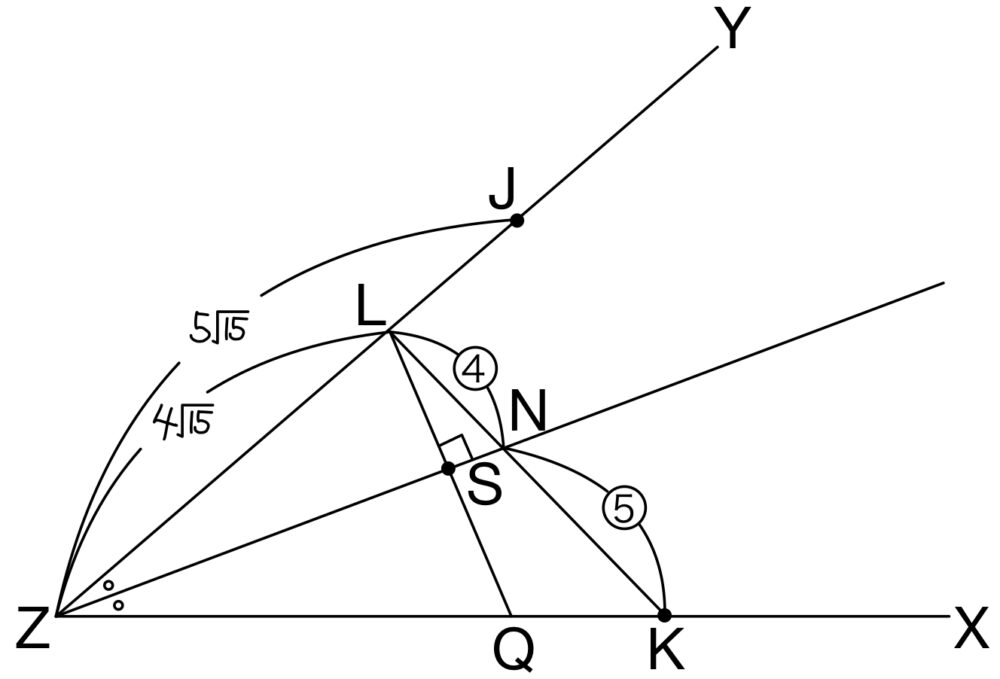
直線 $LS$ と直線 $ZX$ の交点を $Q$ とおく．

メネラウスの定理より

$\displaystyle\frac{ZS}{SN}\times \displaystyle\frac{NL}{LK}\times \displaystyle\frac{KQ}{QZ}=1$

《タチ》の結果から，$\displaystyle\frac{NK}{LK}=\displaystyle\frac{4}{9}$ ．

また $\triangle ZSL≡\triangle ZSQ$ より $ZQ=ZL=4\sqrt{15}$

さらに，$ZJ=ZK=5\sqrt{15}$ であるから，$\displaystyle\frac{KQ}{QZ}=\displaystyle\frac{\sqrt{15}}{4\sqrt{15}}=\displaystyle\frac{1}{4}$

よって，$\displaystyle\frac{ZS}{SN}\times \displaystyle\frac{4}{9}\times \displaystyle\frac{1}{4}=1$

$SN=\displaystyle\frac{1}{9}ZS$ が成り立つ．

直角三角形 $ZLS$ で三平方の定理から

$ZS=\sqrt{ZL^2-LS^2}=\sqrt{ZL^2-LJ^2}=\sqrt{(4\sqrt{15})^2-(\sqrt{15})^2}=$$15$

したがって，$SN=\displaystyle\frac{1}{9}\times 15=$$\displaystyle\frac{5}{3}$ ・・・《ツテ》