【2009京都大学】
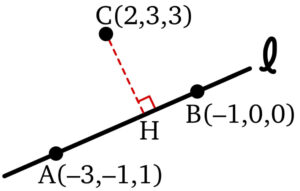
\(xyz\) 平面上の \(2\) 点 \(A(-3,-1,1)\) , \(B(-1,0,0)\) を通る直線 \(l\) に点 \(C(2,3,3)\) から下ろした垂線の足 \(H\) の座標を求めよ.
本問の一般的な解法は,点 \(H\) をパラメータ表示し,\(\overrightarrow{CH}\cdot\overrightarrow{AB}=0\) を利用して解いていくこと(※一般的な模範解答は記事一番下で紹介)ですが,ここでは正射影ベクトルを用いた解法を紹介していきます。
正射影ベクトルとは?
 右図において,
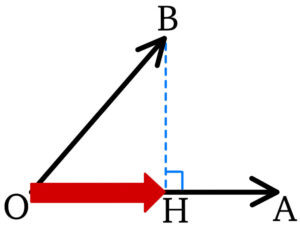
右図において,
\(\overrightarrow{OH}\) を \(\overrightarrow{OB}\) の \(\overrightarrow{OA}\) に対する正射影ベクトルという.
このとき,\(\overrightarrow{OH}\) は \(\overrightarrow{OA}\) , \(\overrightarrow{OB}\) を用いて

真上から光を当てたときに,
スクリーン ( \(\overrightarrow{OA}\) ) にうつる \(\overrightarrow{OB}\) の影というイメージです!
証明

\(3\) 点 \(O\) , \(H\) , \(A\) は一直線上にあるので,
実数 \(k\) を用いて , \(\overrightarrow{OH}=k\overrightarrow{OA}\) とおける.
このとき \(k\) は,\(\overrightarrow{OA}\) , \(\overrightarrow{OH}\) の大きさを用いて
\(k=\displaystyle\frac{\left|\overrightarrow{OH}\right|}{\left|\overrightarrow{OA}\right|}\) ・・・① と表せる.
また \(\triangle OBH\) に注目すると,\(\cos \angle BOH=\displaystyle\frac{\left|\overrightarrow{OH}\right|}{\left|\overrightarrow{OB}\right|}\)
よって,\(\left|\overrightarrow{OH}\right|=\left|\overrightarrow{OB}\right|\cos \angle BOH\)
①に代入すると
\(k=\displaystyle\frac{\left|\overrightarrow{OB}\right|\cos \angle BOH}{\left|\overrightarrow{OA}\right|}\)
分母分子に \(\left|\overrightarrow{OA}\right|\) をかけると
\(k=\displaystyle\frac{\left|\overrightarrow{OA}\right|\left|\overrightarrow{OB}\right|\cos \angle BOH}{\left|\overrightarrow{OA}\right|^2}=\displaystyle\frac{\overrightarrow{OA}\cdot\overrightarrow{OB}}{\left|\overrightarrow{OA}\right|^2}\)
したがって,\(\overrightarrow{OH}=\displaystyle\frac{\overrightarrow{OA}\cdot\overrightarrow{OB}}{\left|\overrightarrow{OA}\right|^2}\overrightarrow{OA}\)
正射影ベクトルを利用した解答・解説
【2009京都大学】
\(xyz\) 平面上の \(2\) 点 \(A(-3,-1,1)\) , \(B(-1,0,0)\) を通る直線 \(l\) に点 \(C(2,3,3)\) から下ろした垂線の足 \(H\) の座標を求めよ.
 考え方
考え方
点 \(H\) の座標を求める
⇒ \(\overrightarrow{OH}\) を求める
⇒ \(\overrightarrow{OH}=\overrightarrow{OA}+\overrightarrow{AH}\) より,\(\overrightarrow{AH}\) を求めれば良い.
⇒ \(\overrightarrow{AH}\) は,\(\overrightarrow{AB}\) の\(\overrightarrow{AC}\) に対する正射影ベクトル
⇒ \(\overrightarrow{AH}=\displaystyle\frac{\overrightarrow{AB}\cdot\overrightarrow{AC}}{\left|\overrightarrow{AB}\right|^2}\overrightarrow{AB}\)
\(\overrightarrow{AB}=(2,1,-1)\) , \(\overrightarrow{AC}=(5,4,2)\) より
\(\left|\overrightarrow{AB}\right|^2=2^2+1^2+(-1)^2=6\) , \(\overrightarrow{AB}\cdot\overrightarrow{AC}=2\times 5+1\times 4+(-1)\times 2=12\)
\(\overrightarrow{AH}=\displaystyle\frac{\overrightarrow{AB}\cdot\overrightarrow{AC}}{\left|\overrightarrow{AB}\right|^2}\overrightarrow{AB}=\displaystyle\frac{12}{6}\overrightarrow{AB}=2\overrightarrow{AB}\)
であるから,
\(\overrightarrow{OH}=\overrightarrow{OA}+\overrightarrow{AH}=\overrightarrow{OA}+2\overrightarrow{AB}\)
よって,\(\overrightarrow{OH}=(-3,-1,1)+2(2,1,-1)=(1,1,-1)\)
したがって,\(H (1,1,-1)\)
参考:一般的な模範解答
点 \(H\) は直線 \(AB\) 上の点なので,実数 \(t\) を用いて
\(\overrightarrow{OH}=\overrightarrow{OA}+t\overrightarrow{AB}\)
\(=(-3,-1,1)+t(2,1,-1)=(2t-3,t-1,-t+1)\)
よって,\(\overrightarrow{CH}=(2t-5,t-4,-t-2)\)
\(\overrightarrow{CH}\cdot\overrightarrow{AB}=0\) より
\(2(2t-5)+(t-4)-(-t-2)=0\)
よって,\(t=2\)
したがって,\(H (1,1,-1)\)






コメント