【2022大阪医科薬科大学・看護・[3]】
解答・解説
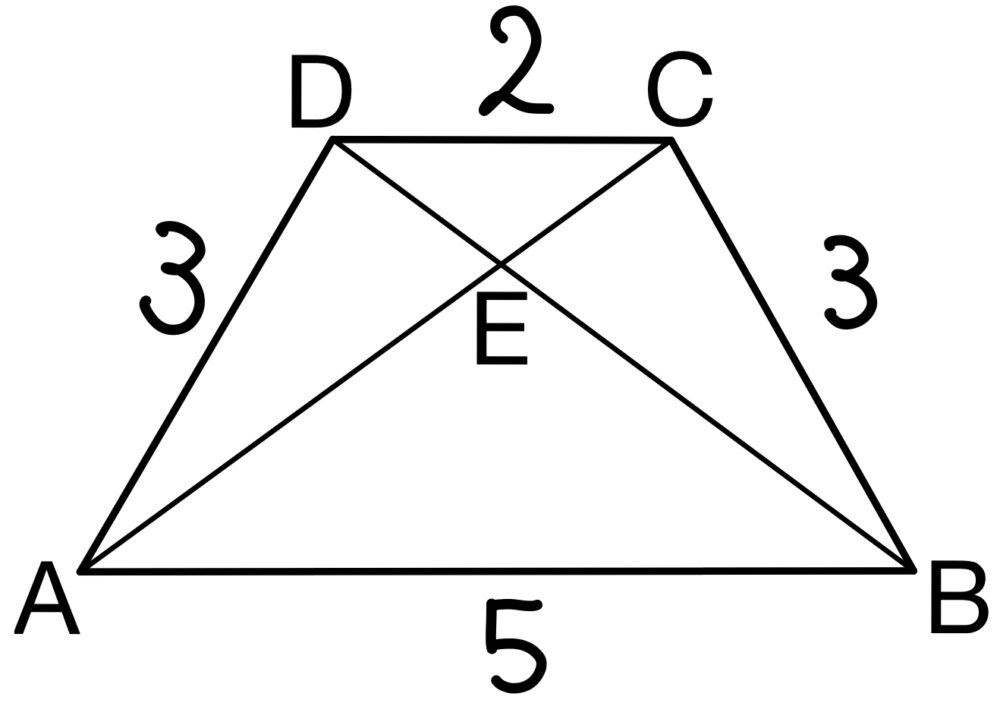
(１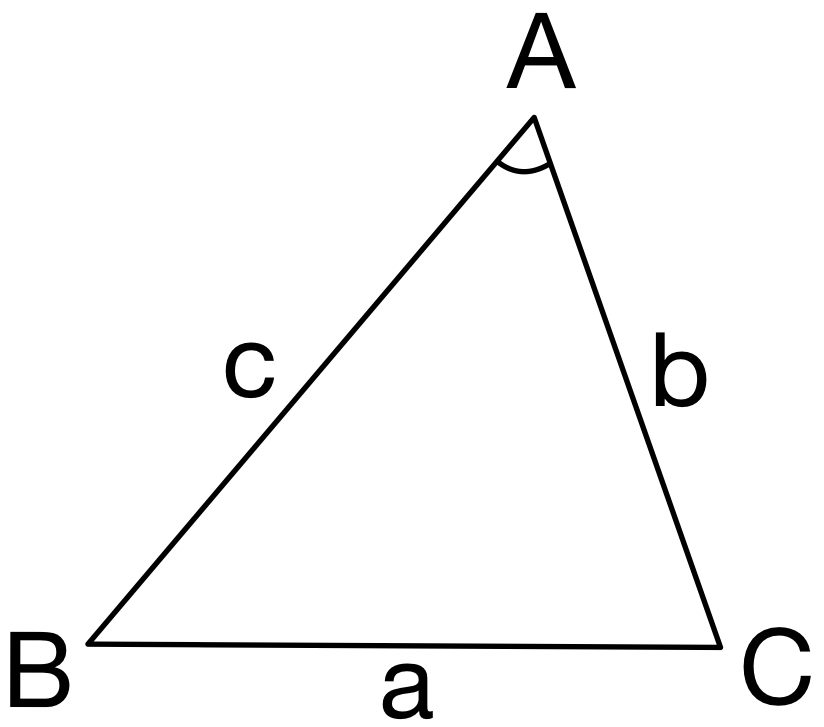) 余弦定理
余弦定理
\(\triangle ABC\) において
・\(a^2=b^2+c^2-2bc\cos A\)
・\(\cos A=\displaystyle\frac{b^2+c^2-a^2}{2bc}\)
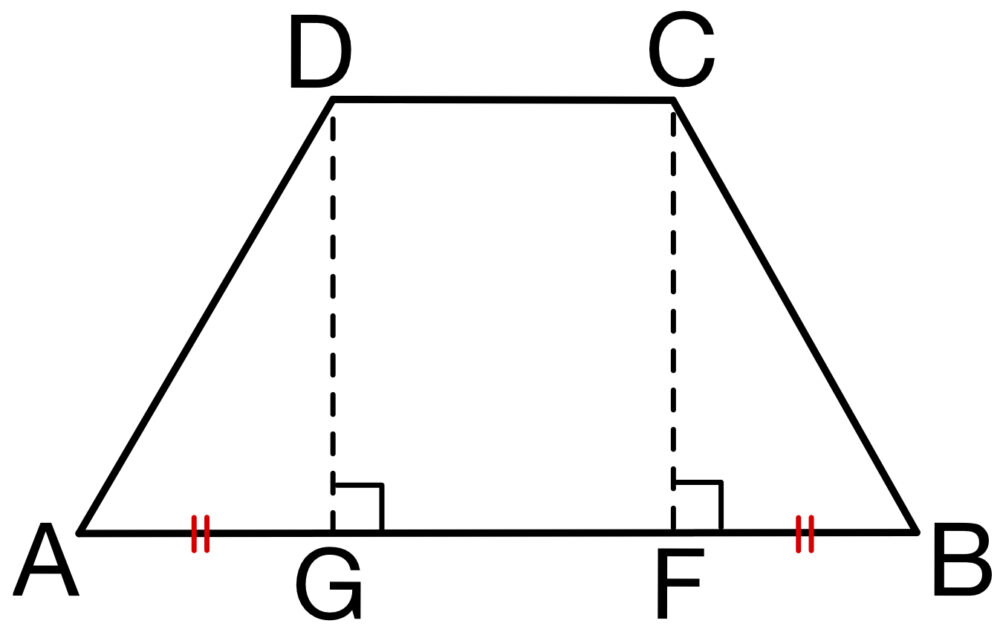
点 \(C\)，\(D\) から線分 \(AB\) に下ろした垂線の足を \( F\)，\(G\) とおくと，
\(CD=FG=2\) であり，
\(AG=BF=\displaystyle\frac{1}{2}(5-2)=\displaystyle\frac{3}{2}\)
ここで \(\triangle ADG\) に注目すると，\(\angle AGD=90°\) で
\(AG：AD=\displaystyle\frac{3}{2}：3=1：2\) より，\(\angle DAG=60°\)
よって，\(\triangle ABD\) で余弦定理より
\(BD^2=5^2+3^2-2\times 5\times 3\times \cos 60°=19\)
\(BD>0\) より \(BD=\sqrt{19}\) ・・・( d )
(２)
\(\angle DAG=60°\) より，\(DG=\sqrt{3}AG=\displaystyle\frac{3\sqrt{3}}{2}\)
よって四角形 \(ABCD\) の面積は
\(\displaystyle\frac{1}{2}\cdot(2+5)\cdot\displaystyle\frac{3\sqrt{3}}{2}=\)\(\displaystyle\frac{21\sqrt{3}}{4}\) ・・・( d )
(３)
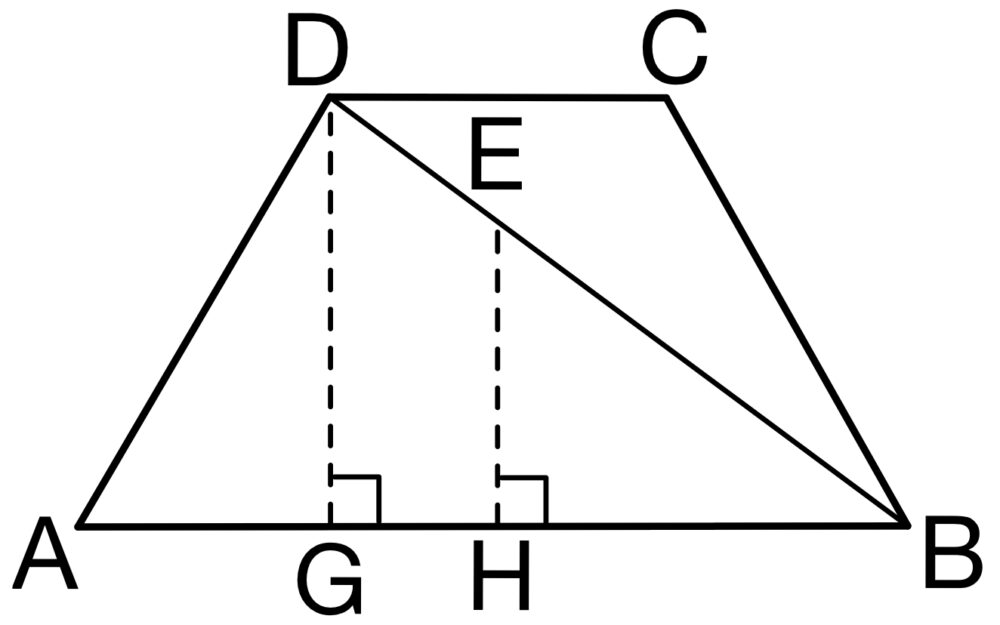
点 \(E\) から線分 \(AB\) に下ろした垂線の足を \(H\) とおくと，
\(\triangle BEH\) と \(\triangle BDG\) は相似である．
よって，\(BE：BH=BD：BG\) ・・・①
ここで，\(BH=\displaystyle\frac{1}{2}AB=\displaystyle\frac{5}{2}\)，
\(BG=AB-AG=\displaystyle\frac{7}{2}\) より①から
\(BE：\displaystyle\frac{5}{2}=\sqrt{19}：\displaystyle\frac{7}{2}\)
\(BE=\displaystyle\frac{5\sqrt{19}}{7}\) ・・・( c )
(４) 四角形の面積(対角線から求める)公式
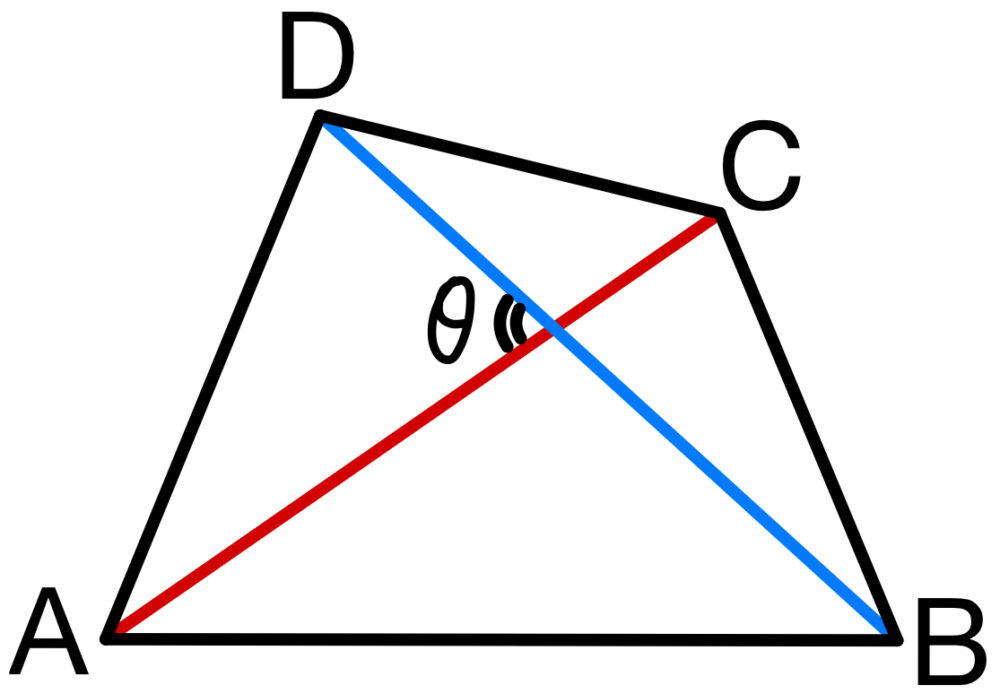対角線を利用した四角形の面積
対角線のなす角を \(\theta\) とするとき，
四角形 \(ABCD\) の面積 \(S\) は，
\(S=\displaystyle\frac{1}{2}AC\times BD\times \sin \theta\)
四角形 \(ABCD\) は等脚台形なので，\(AC=BD=\sqrt{19}\)
(２)より
\(\displaystyle\frac{21\sqrt{3}}{4}=\displaystyle\frac{1}{2}\cdot\sqrt{19}\displaystyle\frac{1}{2}\cdot\sqrt{19}\cdot\sin\angle AED\)
\(\sin\angle AED=\displaystyle\frac{21\sqrt{3}}{38}\) ・・・( e )
コメント