【2020大阪市立大学・文系(一部)】
\(a\) , \(b\) を実数とする.\(3\) 次関数 \(f(x)=x^3+3ax^2+3bx\) に対して,次の問に答えよ.
問1.\(f(x)\) が極大値と極小値をもつための \(a\) , \(b\) の条件を求めよ.
問2.問1の条件が成り立つとする.このとき,\(f(x)\) の極大値の絶対値と極小値の絶対値が等しくなるための \(a\) , \(b\) の条件を求めよ.
極値が存在する条件
極値(極大値・極小値)とは?
関数 \(y=f(x)\) について
[1]\(f^{\prime}(x)\) の符号が \(x=a\) の前後で正から負に変わるとき
\(y=f(x)\) は \(x=a\) で極大になるといい,\(f(a)\) を極大値という.
[2]\(f^{\prime}(x)\) の符号が \(x=b\) の前後で負から正に変わるとき
\(y=f(x)\) は \(x=b\) で極小になるといい,\(f(a)\) を極小値という.
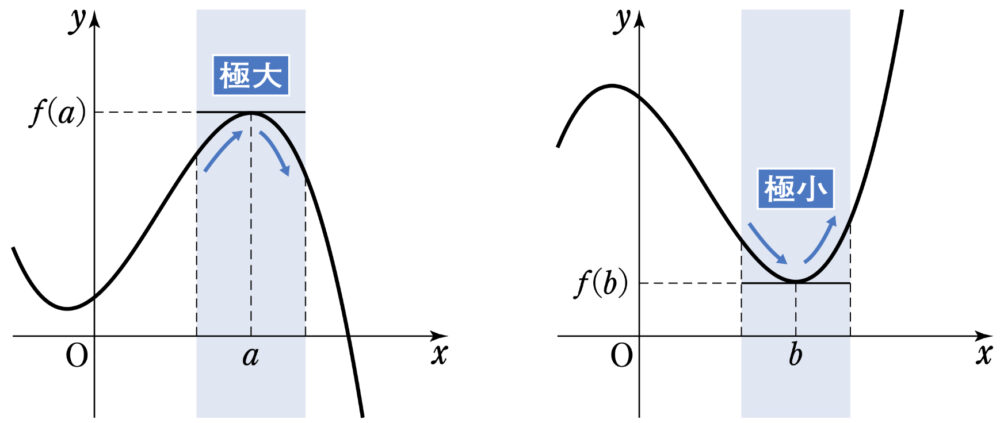
※ 極大値と極小値をまとめて,極値 という.
3 次関数 \(y=f(x)\) が極値をもつ条件
\(3\) 次関数 \(y=f(x)\) が極値をもつ
\(\iff\) \(f^{\prime}(x)=0\) が異なる \(2\) つの実数解をもつ
\(\iff\) \(f^{\prime}(x)=0\) の判別式 \(D\) が,\(D>0\) を満たす
\(y=f(x)\) が \(3\) 次関数であるとき,
\(y=f^{\prime}(x)\) は \(2\) 次関数となり,このグラフが符号変化を起こすためには,
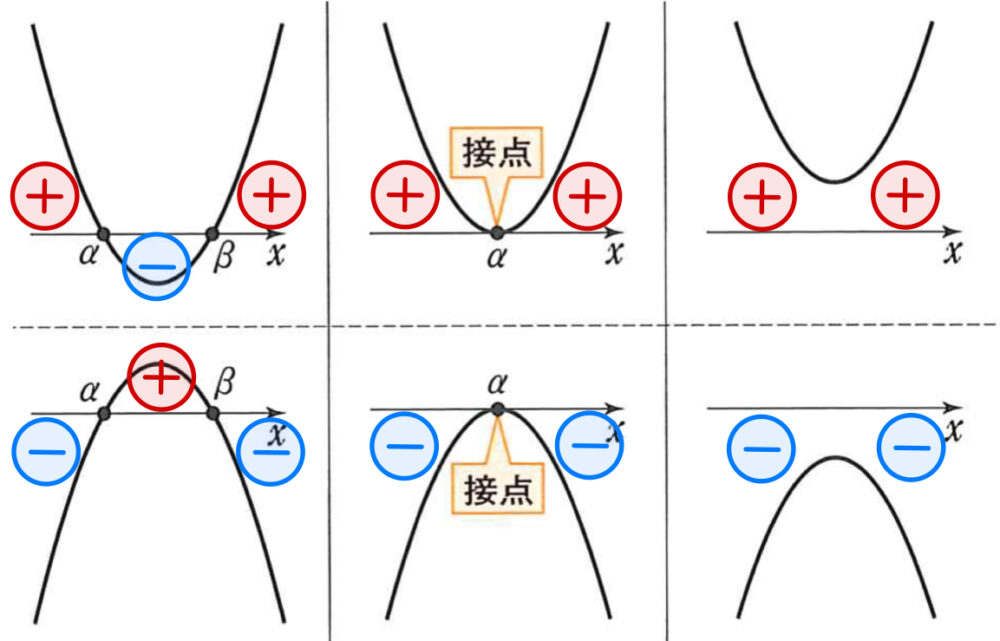
\(y=f^{\prime}(x)\) のグラフが \(x\) 軸と異なる\(2\) 点で交わればよいということである.
極値の和について

解答
問1
\(f(x)=x^3+3ax^2+3bx\) より
\(f^{\prime}(x)=3x^2+6ax+3b\)
\(y=f(x)\) が極値をもつとき,\(f^{\prime}(x)=0\) が異なる \(2\) つの実数解を持てばよいので,
\(f^{\prime}(x)=0\)の判別式を \(D\) とすると
\(\displaystyle\frac{D}{4}=(3a)^2-3\times 3b>0\)
よって,\(b<a^2\)
問2
問1のとき,\(f^{\prime}(x)=3x^2+6ax+3b=0\) の異なる \(2\) つの実数解を \(\alpha\),\(\beta\) とおく.
 ただし,\(\alpha<\beta\) とする.
ただし,\(\alpha<\beta\) とする.
このとき,\(f(\alpha)\) は極大値,\(f(\beta)\) は極小値であり,
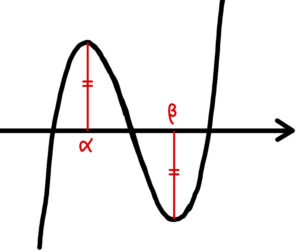
\(f(x)\) の極大値の絶対値と極小値の絶対値が等しくなるとき,
\(f(\alpha)>0>f(\beta)\) であるから,
\(| f(\alpha) | = | f(\beta) |\)
\(\iff\) \(f(\alpha)=-f(\beta)\)
\(\iff\) \(f(\alpha)+f(\beta)=0\) ・・・①
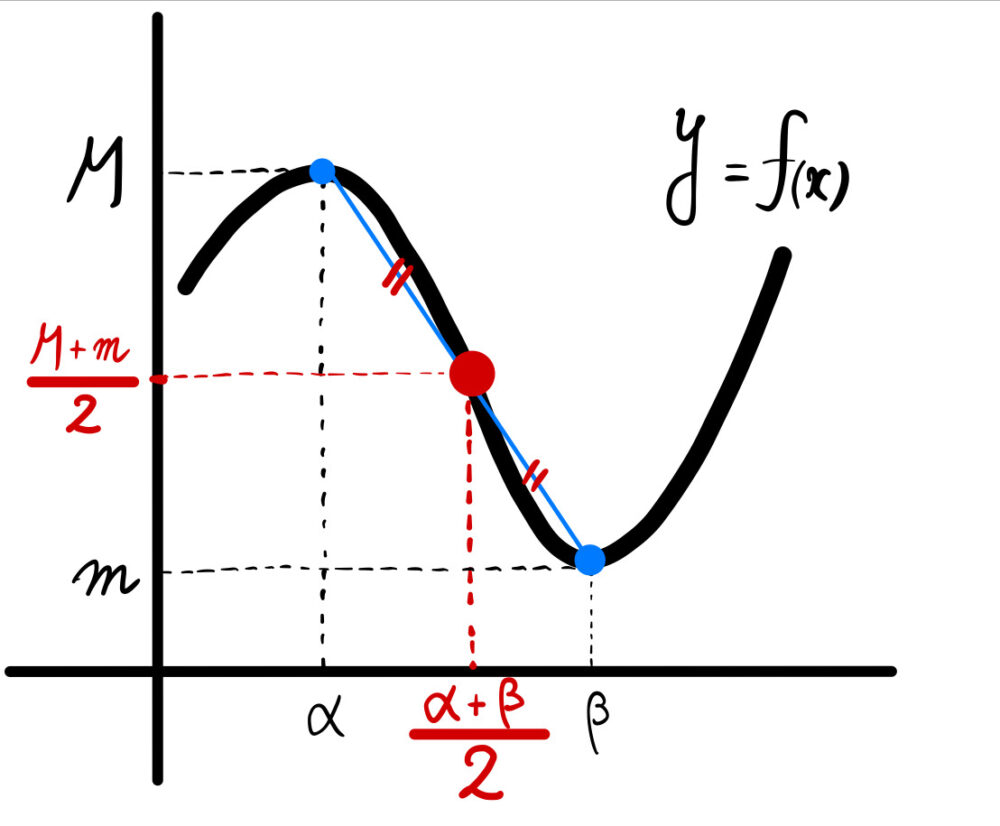
\(3\) 次関数は変曲点に関して対称なグラフであるから
\(\displaystyle\frac{f(\alpha)+f(\beta)}{2}=f\left(\displaystyle\frac{\alpha+\beta}{2}\right)\)
ここで,\(\alpha\),\(\beta\) は \(f^{\prime}(x)=3x^2+6ax+3b=0\) の解であるから,
\(\alpha+\beta=-2a\)
よって,\(\displaystyle\frac{f(\alpha)+f(\beta)}{2}=f(-a)\)
①より,\(f(-a)=0\)
よって,\(-a^3+3a^3-3ab=0\)
\(a(2a^2-3b)=0\)
したがって,\(a=0\) または \(b=\displaystyle\frac{2}{3}a^2\)







コメント