【2022数学ⅠA】第２問[１](2次関数、集合と命題)
(１)(２)問題と解答・解説《ア〜エ》
解答・解説《ア〜エ》
(１)
\(p=4\) , \(q=-4\) のとき
①は \(x^2+4x-4=0\) より
\(x=-2\pm2\sqrt{2}\)
①は \(x^2-4x+4=0\) より
\((x-2)^2=0\)
\(x=2\)
であるから，①または②を満たす実数解の個数は \(n=3\) ・・・《ア》
また，\(p=1\) , \(q=-2\) のとき
①は \(x^2+x-2=0\) より
\((x+2)(x-1)=0\)
\(x=-2,1\)
①は \(x^2-2x+1=0\) より
\((x-1)^2=0\)
\(x=1\)
であるから，①または②を満たす実数解の個数は \(n=2\) ・・・《イ》
(２)
\(p=-6\) のとき
①は \(x^2-6x+q=0\)
②は \(x^2+qx-6=0\)
①，②をともに満たす実数 \(x\) があるとき，それを \(x=\alpha\) とする．
\(\alpha^2-6\alpha+q=0\) ・・・① ‘
\(\alpha^2+q\alpha-6=0\) ・・・② ‘
② ‘ ー ① ‘ より
\((q+6)\alpha-(q+6)=0\)
\((q+6)(\alpha-1)=0\)
\(q=-6\) または \(\alpha=1\)
\(q=-6\) のとき \(p=q\) となり①，②は一致するため \(n=3\) とならない．
よって，\(q\not=-6\) となる．
\(\alpha=1\) のとき
\(1-6+q=0\) \(\iff\) \(q=5\)
このとき
①は \(x^2-6x+5=0\)
\((x-1)(x-5)=0\)
\(x=1,5\)
②は \(x^2+5x-6=0\)
\((x+6)(x-1)=0\)
\(x=-6,1\)
となり確かに \(n=3\) となる．
また，\(n=3\) となるのは
①，②のいずれか一方が重解をもち，他方がこの重解と異なる \(2\) 実解をもてばよい．
・①が重解をもつとき
\(\displaystyle\frac{①の判別式}{4}=(-3)^2-q=0\) \(\iff\) \(q=9\)
このとき
①は \(x^2-6x+9=0\)
\((x-3)^2=0\)
\(x=3\)
②は \(x^2+9x-6=0\)
\(x=\displaystyle\frac{-9\pm\sqrt{105}}{2}\) となり
\(n=3\) となる．
・②が重解をもつとき
(②の判別式)\(=q^2+24>0\) となり不適
したがって，\(q=5,9\) ・・・《ウエ》
(３)問題と解答・解説《オ，カ》
解答・解説《オ，カ》
\(p=-6\) に固定し，\(q\) の値だけを変化させる
\(y=x^2-6x+q=(x-3)^2+q-9\) ・・・③
\(y=x^2+qx-6=\left(x+\displaystyle\frac{q}{2}\right)^2-\displaystyle\frac{q^2}{4}-6\) ・・・④
③のグラフの頂点は \((3,q-9)\) ，④のグラフの頂点は \(\left(-\displaystyle\frac{q}{2},-\displaystyle\frac{q^2}{4}-6\right)\) であるから，\(q\) の値を \(1\) から増加させたとき，
③のグラフの頂点の \(x\) 座標は一定で，\(y\) 座標は増加する．
よって，グラフは上側に動くので，⑥ ・・・《オ》
④のグラフの頂点の \(x\) ，\(y\) 座標はともに減少する．
よって，グラフは左下側に動くので，① ・・・《カ》
(４)問題と解答・解説《キ，ク》
解答・解説《キ，ク》
\(5<q<9\) のとき
(２)より \(q=5\) , \(q=9\) のとき
それぞれのグラフは
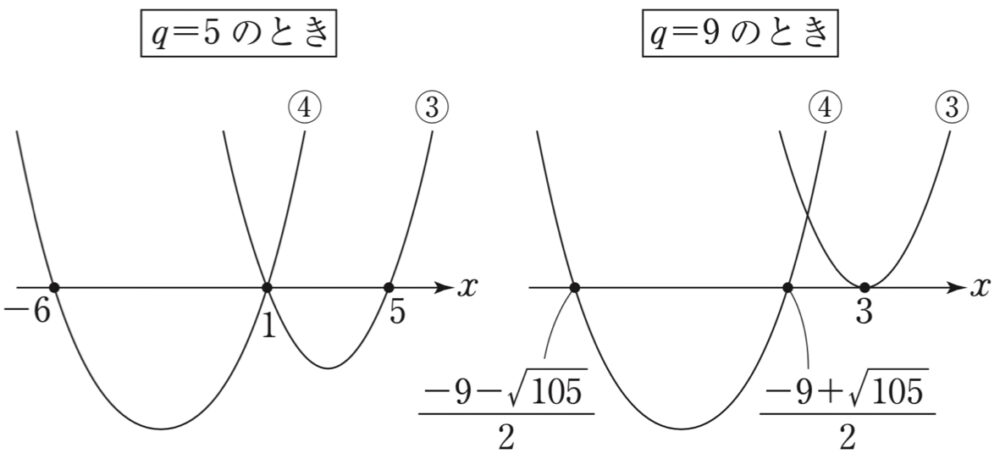
(３)の結果から \(q\) が \(5\) から \(9\) まで動くとき
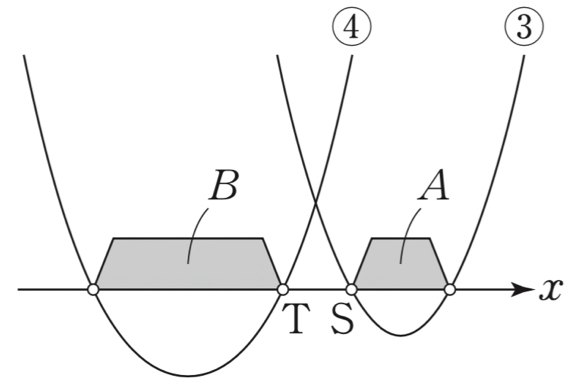③のグラフは上側，④のグラフは左下側に動くことに注意すると
\(A\) と \(B\) は共通範囲を持たず，
常に \(B\) は \(A\) よりも左側にある．
よって，\(A\not\subset B\) であるから
・\(x\in A\) は，\(x\in B\) であるための「③必要条件でも十分条件でもない」・・・《キ》
また，\(B\subset \overline{A}\) であるから
・\(x\in B\) は，\(x\in \overline{A}\) であるための「①十分条件であるが，必要条件ではない」・・・《ク》
コメント