座標平面上に，\(3\) 直線 \(l_{1}\)：\(y=x+1\) , \(l_{2}\)：\(y=2x\) , \(l_{3}\)：\(y=ax+b\) がある．\(l_{1}\) と \(l_{2}\) が \(l_{3}\) に関して対称であるとき，定数 \(a\) , \(b\) の値を求めよ．ただし，\(a>0\) とする．
解答・解説
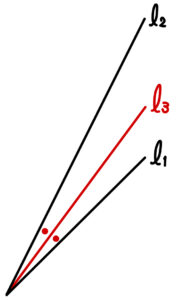\(l_{1}\) ，\(l_{2}\) ，\(l_{3}\) の方向ベクトルをそれぞれ，\(\overrightarrow{d_{1}}\) , \(\overrightarrow{d_{2}}\) , \(\overrightarrow{d_{3}}\) とおくと，
\(\overrightarrow{d_{1}}=(1,1)\) , \(\overrightarrow{d_{2}}=(1,2)\) , \(\overrightarrow{d_{3}}=(1,a)\) と表すことができる．
\(\overrightarrow{d_{1}}\) と \(\overrightarrow{d_{3}}\) のなす角は，\(\overrightarrow{d_{2}}\) と \(\overrightarrow{d_{3}}\) のなす角と等しいので，
\(\displaystyle\frac{\overrightarrow{d_{1}}\cdot\overrightarrow{d_{3}}}{\left|\overrightarrow{d_{1}}\right|\left|\overrightarrow{d_{3}}\right|}=\displaystyle\frac{\overrightarrow{d_{2}}\cdot\overrightarrow{d_{3}}}{\left|\overrightarrow{d_{2}}\right|\left|\overrightarrow{d_{3}}\right|}\)
よって，\(\displaystyle\frac{1+a}{\sqrt{2}\sqrt{1+a^2}}=\displaystyle\frac{1+2a}{\sqrt{5}\sqrt{1+a^2}}\)
これを解くと，\(a=\displaystyle\frac{1+\sqrt{10}}{3}\)
コメント