【2014大阪大学・理系】区分求積法｜1/√nの和の整数部分

考え方

\(\displaystyle\sum_{k=1}^{40000}{\displaystyle\frac{1}{\sqrt{n}}}\)  は計算できるんですか？？

具体的にΣを計算して、値を計算することはできませんよ！

えっ！？

値を計算できないのに、整数部分なんて・・・

そんなことはありませんよ！

今回は「計算しなさい」ではなく、「整数部分」を求めればいいだけです。

例えば、\(3<a<4\) を満たす \(a\) の値は具体的に分からなくても、整数部分は分かりますよね？？

確かに \(3<a<4\) のときの整数部分は \(3\) と分かりますね！

つまり、不等式で挟んであげればいいってことですね！！

でもどうやって・・・

ここでは、教科書にも載っている頻出のテーマである「区分求積法」を利用して考えましょう！

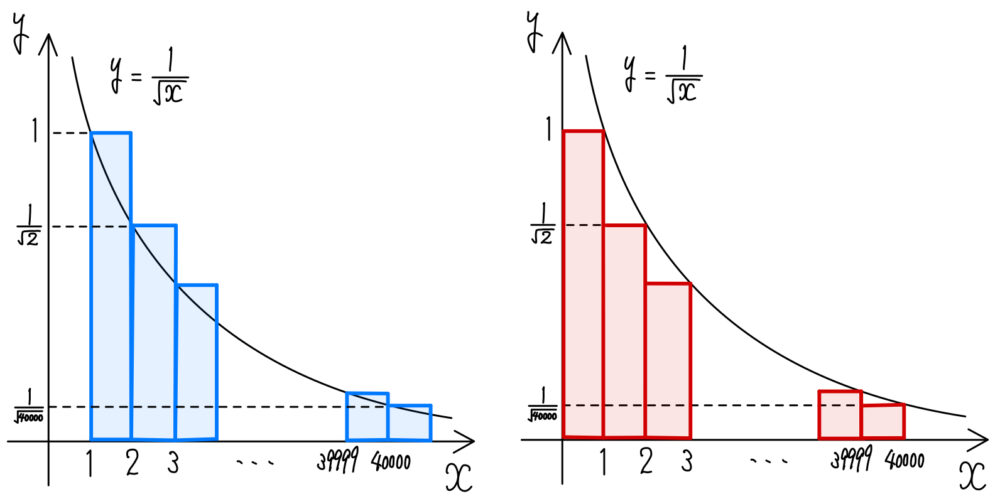
\(y=\displaystyle\frac{1}{\sqrt{n}}\) のグラフと \(x\) 軸でできる幅が \(1\) の長方形の面積(下図参考)を利用して、不等式を作りましょう！！

解答・解説

\(y=\displaystyle\frac{1}{\sqrt{n}}\) のグラフと \(x\) 軸，および直線 \(x=1\) ，\(x=40000\) で囲まれる部分の面積を \(S\) とする．

\(y=\displaystyle\frac{1}{\sqrt{n}}\) ( \(x>0\) ) は，\(y>0\) で単調に減少する関数であり，

\(\displaystyle\sum_{k=1}^{40000}{\displaystyle\frac{1}{\sqrt{n}}}\) は，横の長さが \(1\) ，縦の長さが \(\displaystyle\frac{1}{\sqrt{n}}\) ( \(n=1,2,\cdots,40000\) ) の長方形の面積の和であるから，下図より

\(S+\displaystyle\frac{1}{\sqrt{40000}}<\displaystyle\sum_{k=1}^{40000}{\displaystyle\frac{1}{\sqrt{n}}}\) かつ \(\displaystyle\sum_{k=1}^{40000}{\displaystyle\frac{1}{\sqrt{n}}}<\)\(1+S\)

つまり，\(S+\displaystyle\frac{1}{200}<\displaystyle\sum_{k=1}^{40000}{\displaystyle\frac{1}{\sqrt{n}}}<S+1\)

ここで，

\(S=\displaystyle\int^{40000}_{1}\displaystyle\frac{1}{\sqrt{x}} dx=\Bigl[2\sqrt{x}\Bigr]^{40000}_{1}=2\cdot(200-1)=398\)

したがって，

\(398+\displaystyle\frac{1}{200}<\displaystyle\sum_{k=1}^{40000}{\displaystyle\frac{1}{\sqrt{n}}}<399\) であるから，

\(\displaystyle\sum_{k=1}^{40000}{\displaystyle\frac{1}{\sqrt{n}}}\) の整数部分は \(398\)