【2021数学ⅡB(第２日程)】第２問(微分法・積分法)
[１](１)(２)問題と解答・解説《ア〜エ》
(１)(２)解答・解説《ア〜エ》
\(f(x)=(x-a)(x-2)\)
\(F(x)=\displaystyle\int^{x}_{0}f(t) dt\) より
\(F^{\prime}(x)=f(x)=(x-a)(x-2)\)
(１) \(a=1\) のとき
\(F^{\prime}(x)=(x-1)(x-2)\) より
| \(x\) | ・・・ | \(1\) | ・・・ | \(2\) | ・・・ |
| \(F^{\prime}(x)\) | ＋ | \(0\) | ー | \(0\) | ＋ |
| \(F(x)\) | ↗️ | 極大 | ↘️ | 極小 | ↗️ |
\(x=2\) ・・・《ア》で極小になる．
(２) \(a=2\) ・・・《イ》のとき
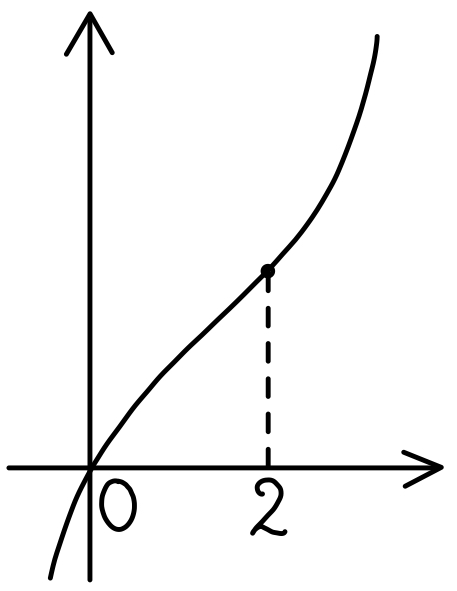\(F^{\prime}(x)=(x-2)^2≧0\) であるから，\(F(x)\) は常に増加する．
また，\(F(0)=\displaystyle\int^{0}_{0}f(t) dt=0\) ・・・《ウ》であるから，
\(y=F(x)\) のグラフは右図のようになるので，
\(F(2)\) の値は，① 正 ・・・《エ》
[１](３)問題と解答・解説《オ〜コ》
(３)解答・解説《オ〜コ》
\(a>2\) とする．
\(b\) は実数とし，\(G(x)=\displaystyle\int^{x}_{b} f(t)dt\) とおく．
\(G(x)=\displaystyle\int^{x}_{0}f(t) dt-\displaystyle\int^{b}_{0}f(t) dt\) より
\(G(x)=F(x)-F(b)\) であるから，
\(y=G(x)\) のグラフは，\(y=F(x)\) のグラフを
\(y\) 軸方向に \(-F(b)\) だけ平行移動したものと一致・・・《オ：①，カ：③》
また，\(G^{\prime}(x)=F^{\prime}(x)=(x-2)(x-a)\) となり，\(a>2\) より
| \(x\) | ・・・ | \(2\) | ・・・ | \(a\) | ・・・ |
| \(G^{\prime}(x)\) | ＋ | \(0\) | ー | \(0\) | ＋ |
| \(G(x)\) | ↗️ | 極大 | ↘️ | 極小 | ↗️ |
\(G(x)\) は，
\(x=2\) ・・・《キ》で極大，\(x=a\) ・・・《ク》で極小になる．
\(G(b)=\displaystyle\int^{b}_{b}f(t) dt=0\) ・・・《ケ》であるから，
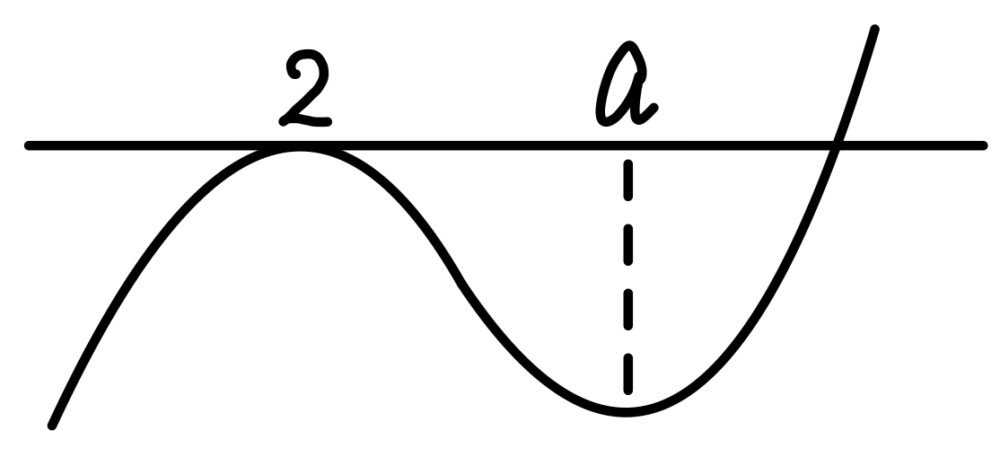\(b=2\) のとき \(G(2)=0\) なので，
\(y=G(x)\) のグラフは右図のようになり，\(y=G(x)\) と \(x\) 軸との共有点の個数は，\(2\) 個・・・《コ》
[２]問題と解答・解説《サ〜テ》
[２]解答・解説《サ〜テ》
\(g(x)=|x|(x+1)\) とおく．
\(x≧0\) のとき，\(g(x)=x(x+1)=x^2+x\)
\(x<0\) のとき，\(g(x)=-x(x+1)=-x^2-x\) より
\(g^{\prime}(x)=\begin{cases}2x+1(x>0)\\-2x-1(x<0) \end{cases}\)
\(g^{\prime}(-1)=-2\times (-1)-1=1\) ・・・《サ》であるから，
\(0<c<1\) のとき，曲線 \(y=g(x)\) と直線 \(l\) : \(y=c(x+1)\) は \(3\) 点で交わる．
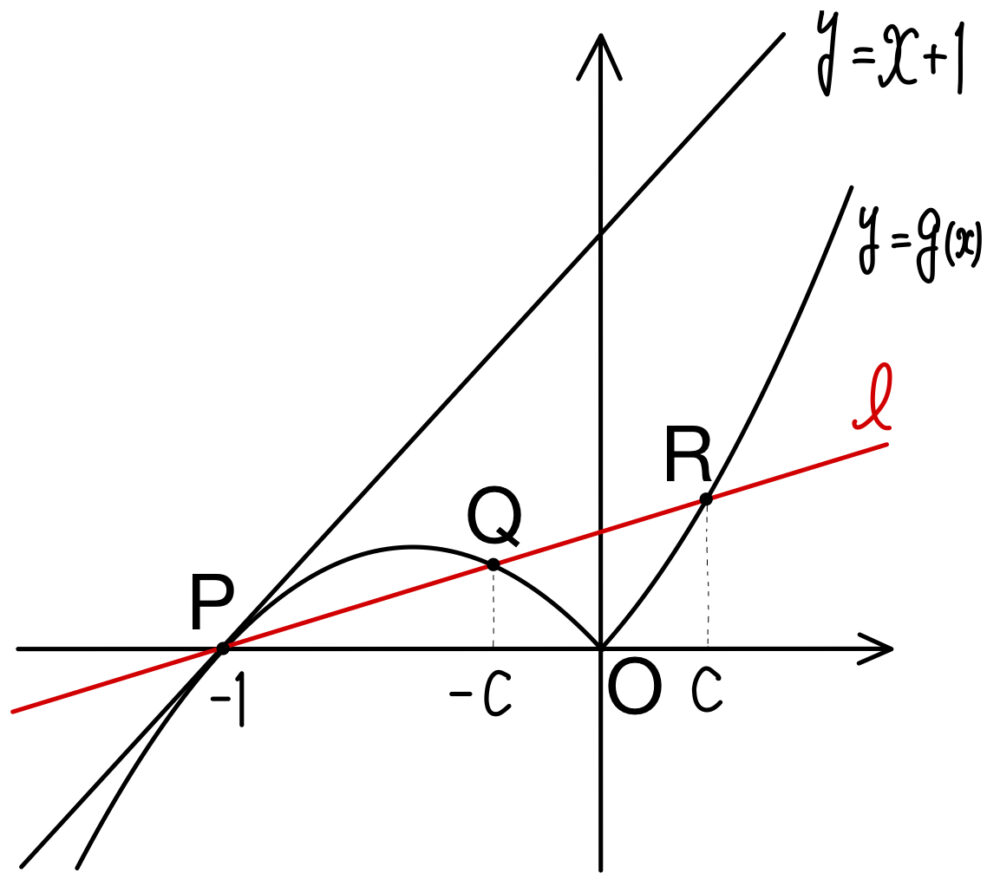このとき，\(Q\) の \(x\) 座標は
\(-x(x+1)=c(x+1)\)
\(x+1\not=0\) より，\(x=-c\) ・・・《シス》
\(R\) の \(x\) 座標は
\(x(x+1)=c(x+1)\)
\(x+1\not=0\) より，\(x=c\) ・・・《セ》
\(0<c<1\) のとき
線分 \(PQ\) と \(y=g(x)\) で囲まれた図形の面積 \(S\) は，
\(S=\displaystyle\int^{-c}_{-1}\left\{-x(x+1)-c(x+1)\right\}dx=\displaystyle\int^{-c}_{-1}-(x+1)(x+c) dx\)
\(=\displaystyle\frac{1}{6}\left\{-c-(-1)\right\}^3=\)\(\displaystyle\frac{-c^3+3c^2-3c+1}{6}\) ・・・《ソ〜ツ》
また，線分 \(QR\) と \(y=g(x)\) で囲まれた図形の面積 \(T\) は，
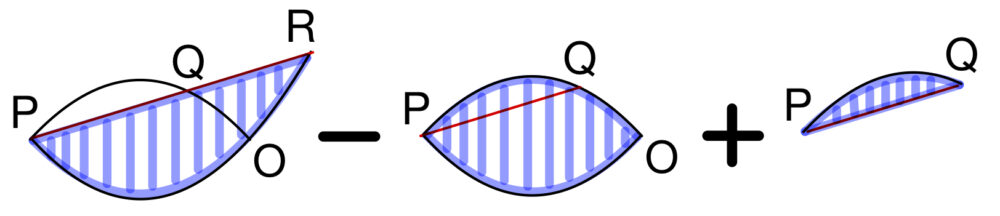
\(\displaystyle\int^{c}_{-1}\left\{c(x+1)-x(x+1)\right\} dx-\displaystyle\int^{0}_{-1}\left\{-x(x+1)-x(x+1)\right\} dx+S\)
\(=-\displaystyle\int^{c}_{-1}(x+1)(x+c) dx+2\displaystyle\int^{0}_{-1}x(x+1) dx+S\)
\(=\displaystyle\frac{1}{6}(c+1)^3-\displaystyle\frac{2}{6}(1-0)^3+\displaystyle\frac{1}{6}(-c+1)^3\)
したがって，\(T=c^2\) ・・・《テ》
コメント