【2019京都大学(文理共通)第5問】
半径 \(1\) の球面上の \(5\) 点 \(B_{1}\),\(B_{2}\),\(B_{3}\),\(B_{4}\) は,正方形 \(B_{1}B_{2}B_{3}B_{4}\) を底面とする四角錐をなしている.この \(5\) 点が球面上を動くとき,四角錐 \(AB_{1}B_{2}B_{3}B_{4}\) の体積の最大値を求めよ.
解答・解説
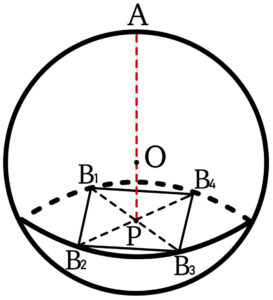
正方形 \(B_{1}B_{2}B_{3}B_{4}\) の対角線の交点を \(P\) ,
球の中心を \(O\) とする.
底面の正方形 \(B_{1}B_{2}B_{3}B_{4}\) を固定したとき,
四角錐 \(AB_{1}B_{2}B_{3}B_{4}\) の体積が最大となるのは,
\(3\) 点 \(A\) , \(O\) , \(P\) がこの順で一直線上にあるときである.
このとき \(OP=h\) とおく ( \(0≦h<1\) )
\(B_{1}P=\sqrt{OB^2_{1}-OP^2}=\sqrt{1-p^2}\) より
正方形の \(1\) 辺の長さは,\(\sqrt{2}\sqrt{1-p^2}\) であるから,
正方形 \(B_{1}B_{2}B_{3}B_{4}\) の面積は
\(\left(\sqrt{2}\sqrt{1-p^2}\right)^2=2(1-p^2)\)
また,\(AP=1+p\) より
四角錐の体積を \(V\) とすると
\(V=\displaystyle\frac{1}{3}\times 2(1-p^2)(1+p)\)
\(V=\displaystyle\frac{-2}{3}(p^3+p^2-p-1)\)
\(V^{\prime}=\displaystyle\frac{-2}{3}(3p^2+2p^2-1)=\displaystyle\frac{-2}{3}(p+1)(3p-1)\)
\(0≦p<1\) に注意すると
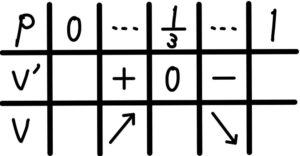
増減表より, \(p=\displaystyle\frac{1}{3}\) のとき最大値は \(\displaystyle\frac{64}{81}\)







コメント