【2022数学ⅠA】第１問[２](図形と計量)

問題と解答・解説《コ〜セ》

解答・解説《コ〜セ》

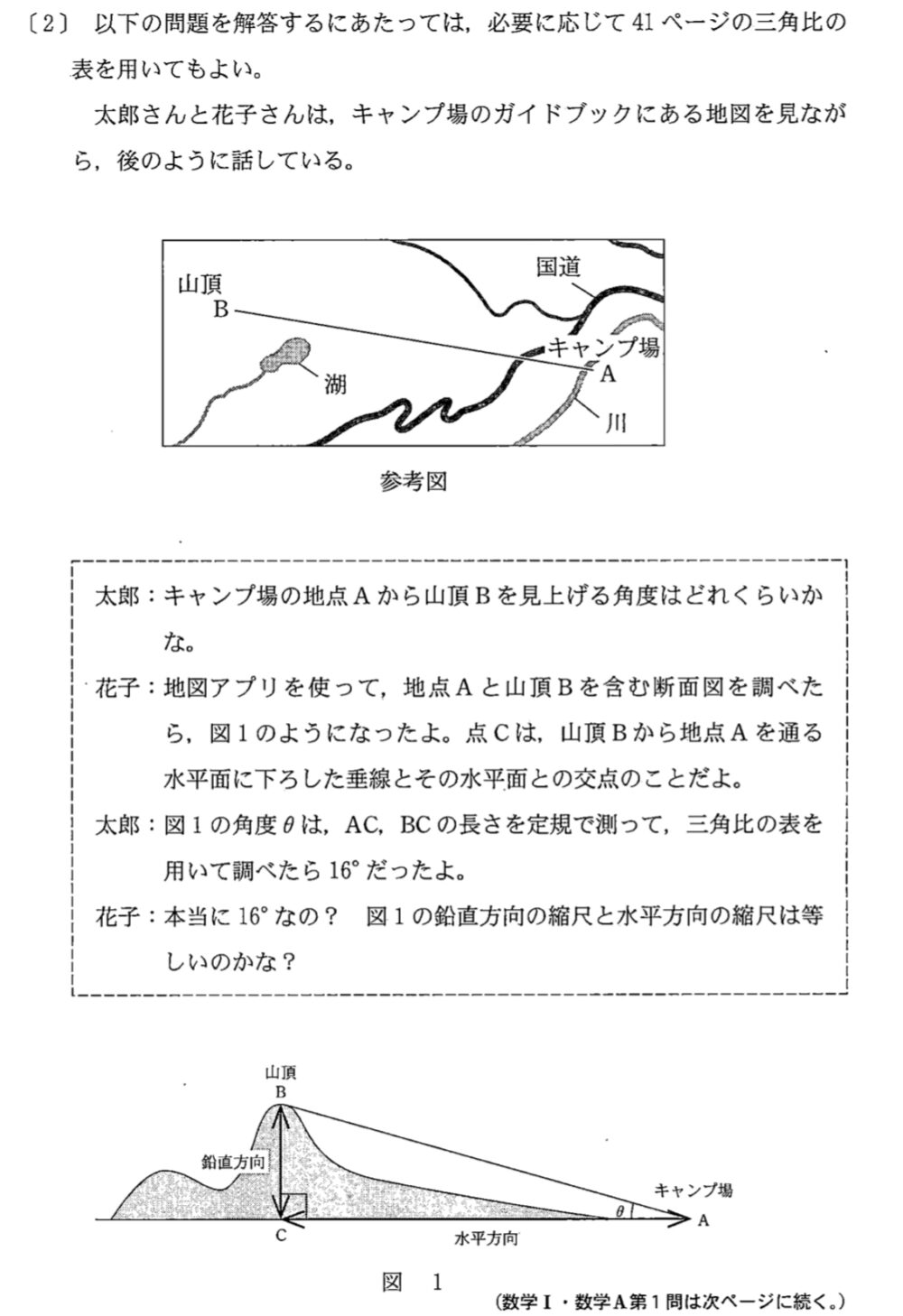
図 \(1\) において， \(AC=x\) , \(BC=y\) とおくと，

\(\tan\angle BAC=\displaystyle\frac{y}{x}=\tan 16°\) で

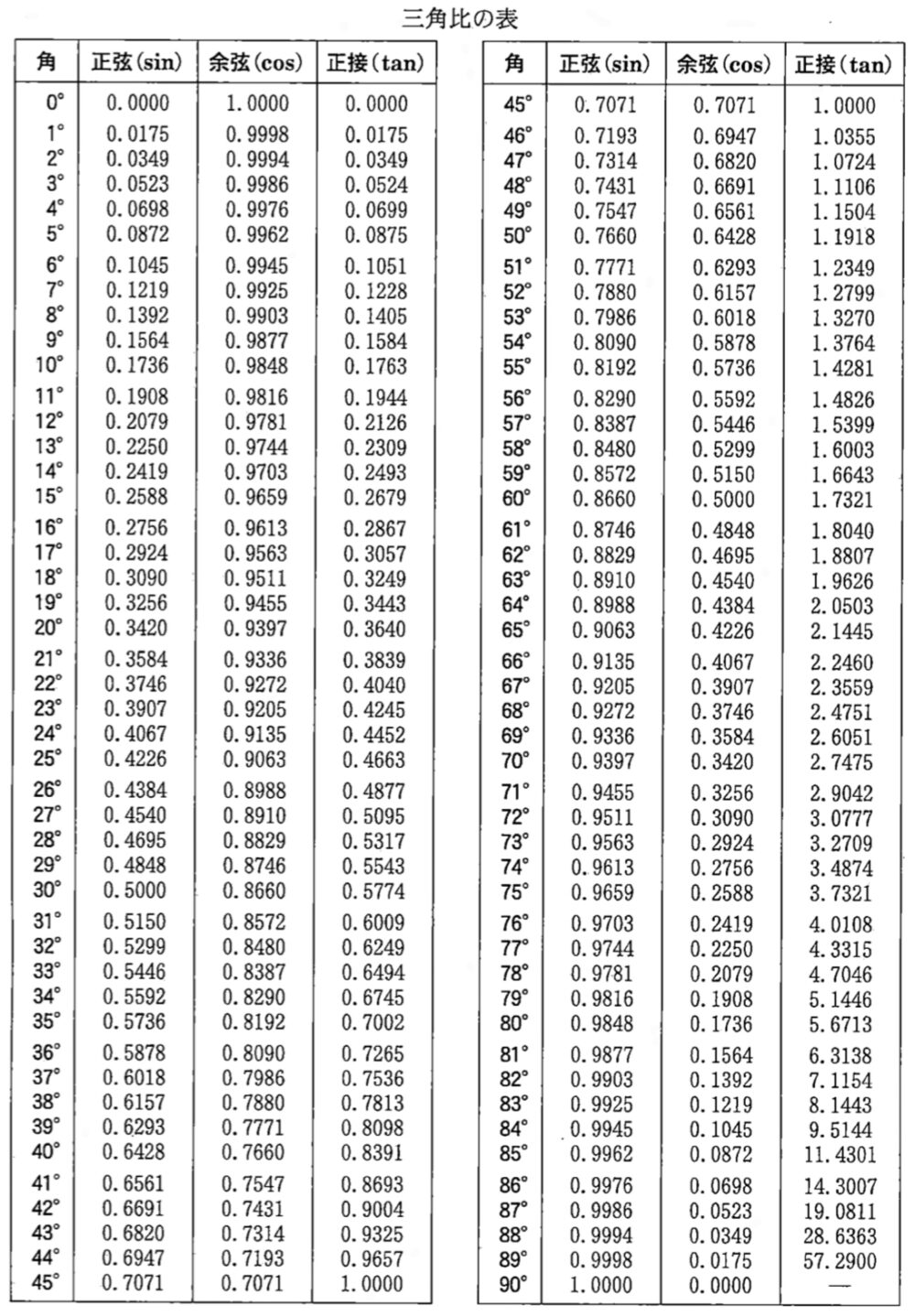
三角比の表から \(\tan 16°=0.2867\) より

\(\displaystyle\frac{y}{x}=0.2867\) ・・・①

図 \(1\) の縮尺は水平方向に \(\displaystyle\frac{1}{100000}\) , 鉛直方向に \(\displaystyle\frac{1}{25000}\) なので

実際の長さは \(AC=100000x\) , \(BC=25000y\) であるから①より

\(\tan \angle BAC=\displaystyle\frac{25000y}{100000x}=\displaystyle\frac{y}{4x}=\displaystyle\frac{1}{4}\times 0.2867≒\)\(0.072\) ・・・《コ〜ス》

三角比の表より

\(\tan 4°=0.0699\) , \(\tan 5°=0.0875\) であるから

\(\tan 4°<\tan \angle BAC<\tan 5°\) より

\(\angle BAC\) は \(4°\) より大きく \(5°\) より小さい・・・《セ：②》

【2022共通テスト】数学ⅠA：第１問[１](数と式)｜対称式の計算問題

２文字、３文字の２乗の和に関する対称式の計算。大学共通テスト対策。センター試験過去問演習。数学ⅠA数と式

mathmathmanabu.com

2022.08.25

【2022共通テスト】数学ⅠA：第１問[３](図形と計量)｜正弦定理・三角比の定義

外接円の半径が与えられた三角形について。正弦定理、三角比の定義を利用。(1)は具体的な2辺の長さについて。(2)は2辺の長さの関係式から考える。(1)の流れがヒントになっている、共通テスト独特の問題。大学共通テスト対策。センター試験過去問演習。数学ⅠA：図形と計量

mathmathmanabu.com

2022.08.27