【2020東京電機大・理工】
\(3\) 次関数 \(f(x)\) は \(x=-1\) で極大値 \(7\) をとり,\(x=3\) で極小値 \(-25\) をとる.
\(f(x)\) を求めよ.
\(x=a\) で極値をもつとき(逆の確認を!)
\(x=a\) で極値をもつ \(\Rightarrow\) \(f^{\prime}(a)=0\)
※ 逆の「 \(f^{\prime}(a)=0\) \(\Rightarrow\) \(x=a\) で極値をもつ 」に関しては,成り立つとは限らない.
反例:\(f(x)=x^3\)
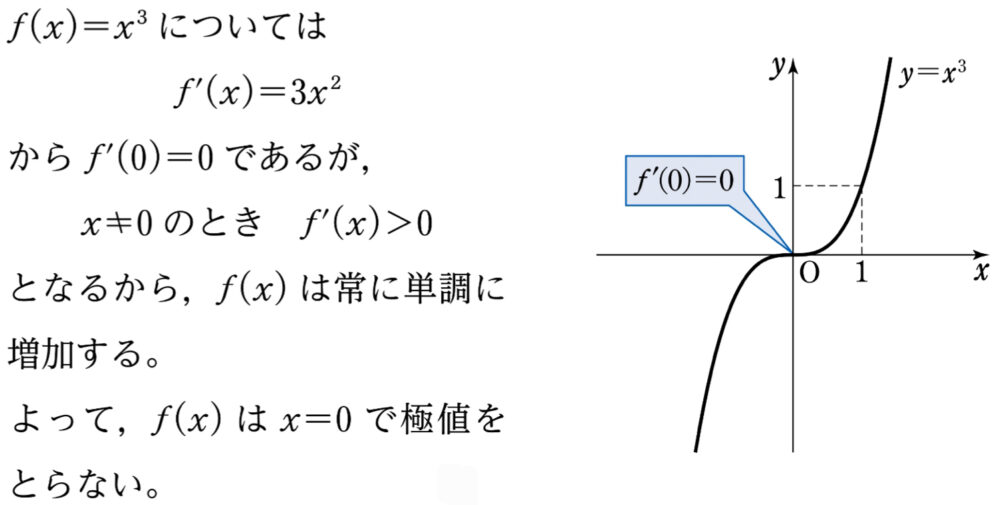

逆に関しては成り立たないことがあるため,
最後に逆の確認(十分条件)の確認を忘れないように!
解答・解説
\(a\not=0\) とし,\(f(x)=ax^3+bx^2+cx+d\) とすると,
\(f^{\prime}(-1)=0\) , \(f^{\prime}(3)=0\) であるから
\(3a-2b+c=0\) ・・・①
\(27a+6b+c=0\) ・・・②
② ー ①から \(24a+8b=0\)
よって,\(b=-3a\) ・・・③
①に③を代入すると,\(c=-9a\) ・・・④
③,④より \(f(x)=ax^3-3ax^2-9ax+d\)
また,\(f(-1)=7\) , \(f(3)=-25\) であるから
\(5a+d=7\) , \(-27a+d=-25\) より
\(a=1\) , \(d=2\)
③,④より \(b=-3\) ,\(c=-9\)

ここで答えとしたら減点されます!
逆の確認(十分条件)の確認を忘れずに!
このとき逆に,\(f(x)=x^3-3x^2-9x+2\) であるから
\(f^{\prime}(x)=3x^2-6x-9=3(x+1)(x-3)\) より増減表は次のようになる.
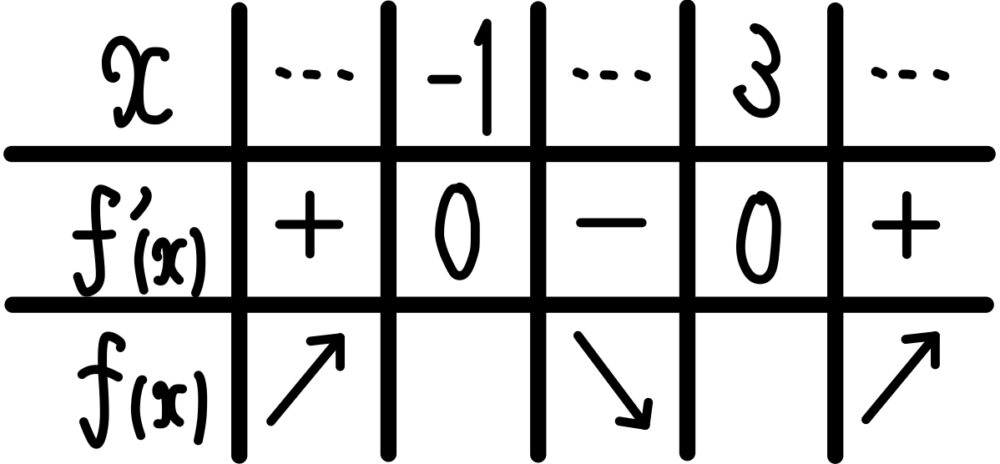
よって確かに,
ゆえに,\(3\) 次関数 \(f(x)\) は \(x=-1\) で極大値 ,\(x=3\) で極小値をもつ
したがって,\(f(x)=x^3-3x^2-9x+2\)







コメント