【2019防衛医科大学校】
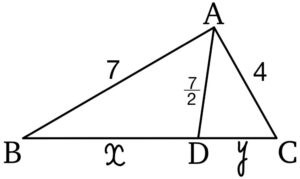
\(AB=7\) , \(AC=4\) である \(\triangle ABC\) において , 辺 \(BC\) 上に \(AD=\displaystyle\frac{7}{2}\) となる点 \(D\) をとる.このとき,\(BD\) はいくらか.ただし,\(BC\) , \(BD\) は自然数とする.
三角形の成立条件・存在条件
\(a\) , \(b\) , \(c\) が三角形の \(3\) 辺となるための条件は
\(| b-c |<a<b+c\)
が成り立つこと

①相加・相乗平均の関係
②コーシー・シュワルツの不等式
③三角不等式(三角形の成立条件)
の3つの不等式は受験数学で覚えておきたい有名不等式になります!
相加平均・相乗平均の関係については「相加平均・相乗平均の関係はいつ使う?使うタイミングの見抜き方(発展)」
整数問題のPoint
まず整数問題すべてに共通して言えるPointは
- 積の形に変形
- 条件から範囲を絞る
- 倍数や余りに注目
整数問題の多くが、上の1から3のいずれかで処理できます。
本問では,三角形の成立条件から範囲を絞り,また関係式において倍数に注目して処理しましょう!
解答・解説
 \(x\) , \(y\) を自然数として
\(x\) , \(y\) を自然数として
\(BD=x\) , \(DC=y\) とおく.
\(\triangle ABD\) , \(\triangle ACD\) , \(\triangle ABC\) について,
三角形の成立条件より
\(\begin{cases}7-\displaystyle\frac{7}{2}<x<7+\displaystyle\frac{7}{2}\\4-\displaystyle\frac{7}{2}<y<4+\displaystyle\frac{7}{2}\\7-4<x+y<7+4\end{cases}\)
\(\begin{cases}\displaystyle\frac{7}{2}<x<\displaystyle\frac{21}{2}\\\displaystyle\frac{1}{2}<x<\displaystyle\frac{15}{2}\\3<x+y<11\end{cases}\)
\(x\) , \(y\) は自然数であるから,
\(4≦x≦10\) ・・・①
\(1≦y≦7\) ・・・②
\(4≦x+y≦10\) ・・・③
ここで,\(\angle ADB=\theta\) とおくと \(\angle ADC=180°-\theta\) であり,
\(\cos (180°-\theta)=-\cos \theta\) であるから \(\triangle ABD\) , \(\triangle ACD\) において 余弦定理より
\(\displaystyle\frac{\left(\displaystyle\frac{7}{2}\right)^2+x^2-7^2}{2\cdot\displaystyle\frac{7}{2}\cdot x}=-\displaystyle\frac{\left(\displaystyle\frac{7}{2}\right)^2+y^2-4^2}{2\cdot\displaystyle\frac{7}{2}\cdot y}\)
これを整理して
\(4x^2y+4xy^2=15x+147y\)
\(\iff\) \(4xy(x+y)-4(4x+37y)=-(x+y)\) ・・・④
④の左辺は \(4\) の倍数であるから,\(x+y\) は \(4\) の倍数となる.
①〜③より,\(x+y=8\)・・・⑤
④に代入すると,\(8xy-4x-37y=-2\)
\(2\left\{2(2xy-x)+1\right\}=37y\)
\(2\) と \(37\) は互いに素であり,左辺は \(4\) の倍数とならない.
よって,\(y\) は \(2\) の倍数かつ \(4\) の倍数ではない・・・⑥ となる.
①,②,⑤,⑥から
よって,\(( x , y ) = ( 6 , 2 )\)
これはすべての条件を確かに満たす.
したがって,\(BD=6\)







コメント