【2022大阪大学・文】放物線と直線が囲む図形の面積の最小値(数Ⅱ：微分積分)

(１)放物線と直線で囲まれた図形の面積(6分の1公式)

\(\displaystyle\int^{\beta}_{\alpha}(x-\alpha)(x-\beta)dx\)

\(x-\alpha\) の形を作るために，

\(x-\beta\) を \(x\)\(-\alpha+\alpha\)\(-\beta\) として式変形！

\(=\displaystyle\int^{\beta}_{\alpha}(x-\alpha)\left\{(x-\alpha)-(\beta-\alpha)\right\}dx\)

\(=\displaystyle\int^{\beta}_{\alpha}\left\{(x-\alpha)^2-(\beta-\alpha)(x-\alpha)\right\}dx\)

\(1\) 次式の \(n\) 乗の積分

\(\displaystyle\int (ax+b)^n dx=\displaystyle\frac{1}{a(n+1)}(ax+b)^{n+1}+C\)

\(=\Bigl[\displaystyle\frac{1}{3}(x-\alpha)^3-\displaystyle\frac{\beta-\alpha}{2}(x-\alpha)^2\Bigr]^{\beta}_{\alpha}\)

\(=\displaystyle\frac{1}{3}(\beta-\alpha)^3-\displaystyle\frac{1}{2}(\beta-\alpha)^3\)

\(=\displaystyle\frac{(\alpha-\beta)^3}{6}\)

(２)面積の最小値

直線 \(l\) は点 \(A\) を通り，傾きが \(k\) の直線より

\(y-b=k(x-a)\) \(\iff\) \(y=kx-ak+b\) ・・・①

\(y=x^2\) と①より

\(x^2=kx-ak+b\)

\(x^2-kx+ak-b=0\) ・・・②

②の判別式を \(D\) とするとき

\(D=k^2-4(ak-b)=(k-2a)^2+4(b-a^2)\)

\((k-2a)^2≧0\) , \(b-a^2>0\) より

\(D>0\) であるから，②は異なる \(2\) つの実数解をもつ．

これらを \(\alpha\)，\(\beta\) とおく( \(\alpha<\beta\) )

解と係数の関係から，

\(\alpha+\beta=k\) , \(\alpha\beta=ak-b\) ・・・③

解と係数の関係を利用する際は，しっかりと \(2\) 次方程式が解をもつこと(判別式が

正または0)であることを確認するように！

このとき，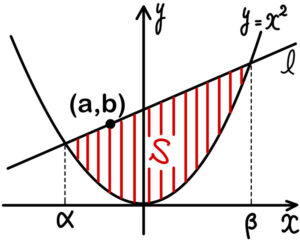

\(S(k)=\displaystyle\int^{\beta}_{\alpha}\left\{(kx-ak+b)-x^2\right\}dx\)

\(=-\displaystyle\int^{\beta}_{\alpha}\left\{(x-\alpha)(x-\beta)\right\}dx\)

(１)より

\(S(k)=\displaystyle\frac{(\beta-\alpha)^3}{6}\)

\(=\displaystyle\frac{1}{6}\left\{(\beta-\alpha)^2\right\}^{\frac{3}{2}}\) ・・・④

ここで，

\((\beta-\alpha)^2=(\alpha+\beta)^2-4\alpha\beta\) より③を代入すると

\((\beta-\alpha)^2=k^2-4(ak-b)\)

\(=(k-2a)^2+4(b-a^2)\) より

\(k=2a\) のとき④は最小となる．

したがって求める最小値は

\(S(2a)=\displaystyle\frac{1}{6}\left\{4(b-a^2)\right\}^{\frac{3}{2}}=\displaystyle\frac{4}{3}(b-a^2)^{\frac{3}{2}}\)