【2021札幌医科大学・医学部】sinC=2cosAsinBはどのような三角形？

【2021札幌医科大学・医学部・第１問(１)】

三角形 \(ABC\) において

\(\sin C=2\cos A\sin B\)

であるとき，三角形 \(ABC\) はどのような形をしているか．

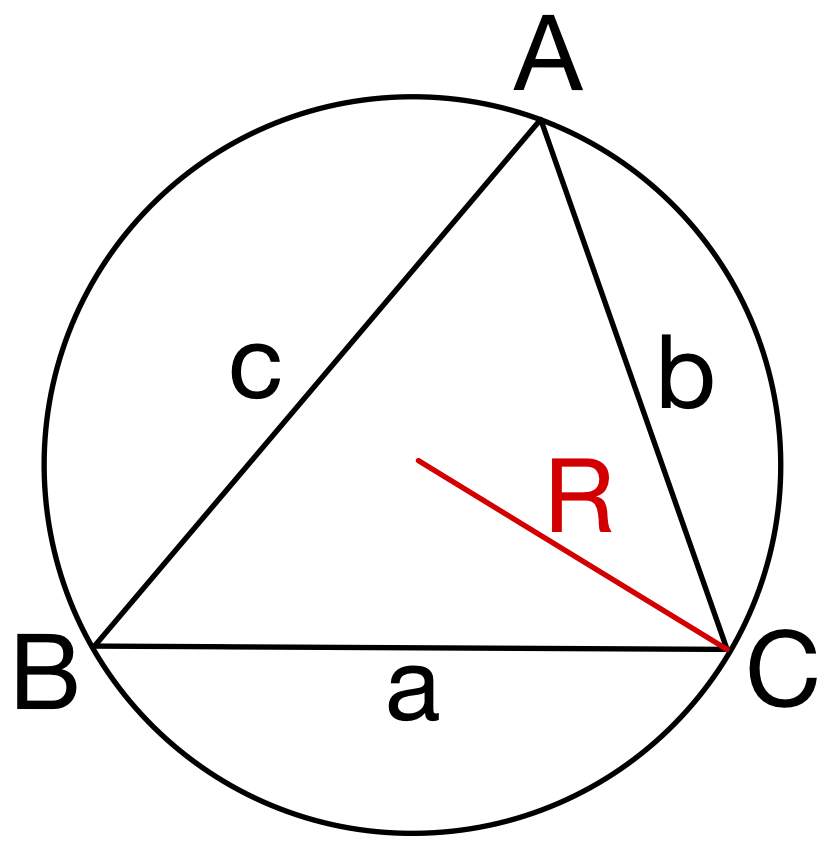正弦定理・余弦定理

正弦定理
\(\triangle ABC\) の外接円半径を \(R\) とする．

\(2R=\displaystyle\frac{a}{\sin A}=\displaystyle\frac{b}{\sin B}=\displaystyle\frac{c}{\sin C}\)

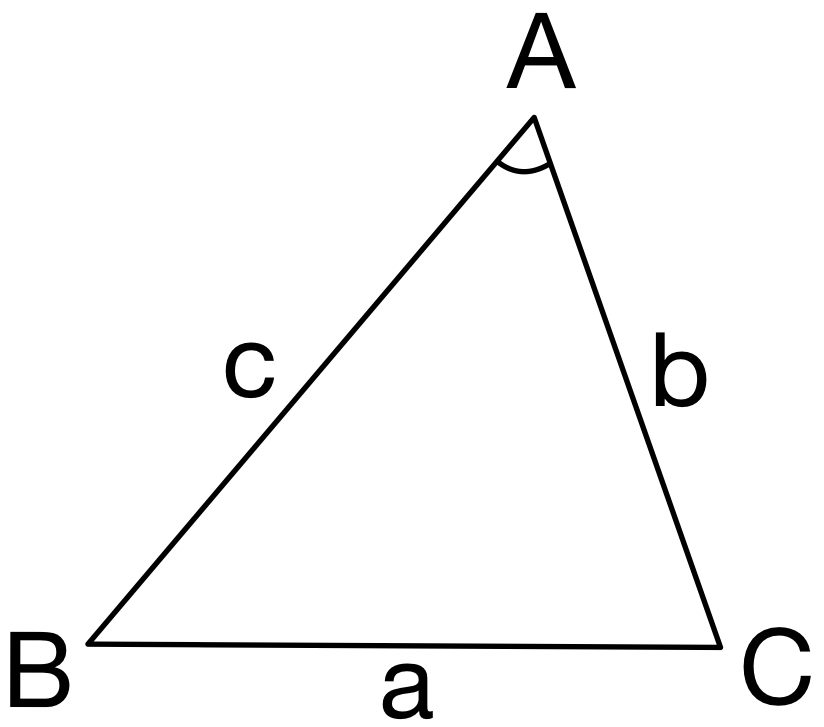余弦定理

\(\triangle ABC\) において

・\(a^2=b^2+c^2-2bc\cos A\)

・\(\cos A=\displaystyle\frac{b^2+c^2-a^2}{2bc}\)

辺 \(BC\)，\(CA\)，\(AB\) の長さをそれぞれ \(a\) ，\(b\)，\(c\) とおく．

正弦定理より

\(\displaystyle\frac{b}{\sin B}=\displaystyle\frac{c}{\sin C}\)

よって，\(\sin C=\displaystyle\frac{c}{b}\sin B\) ・・・①

また余弦定理より

\(\cos A=\displaystyle\frac{b^2+c^2-a^2}{2bc}\) ・・・②

①，②を与式に代入すると，

\(\displaystyle\frac{c}{b}\sin B=2\cdot\displaystyle\frac{b^2+c^2-a^2}{2bc}\cdot\sin B\)

\(\sin B\not=0\) より

\(c=\displaystyle\frac{b^2+c^2-a^2}{c}\)

よって，\(a^2=b^2\)

\(a>0,b>0\) より，\(a=b\)

したがって，三角形 \(ABC\) は，\(BC=CA\) を満たす二等辺三角形．