【2007大阪大学】
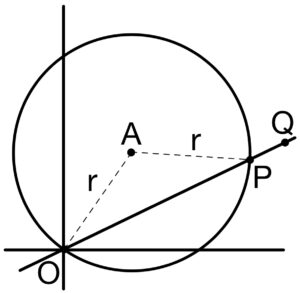
\(xy\) 平面において,原点 \(O\) を通る半径 \(r\) ( \(r>0\) ) の円を \(C\) とし,その中心を \(A\) とする.\(O\) を除く \(C\) 上の点 \(P\) に対し,次の条件 \((a)\) , \((b)\) で定まる点 \(Q\) を考える.
\((a)\) \(\overrightarrow{OP}\) と \(\overrightarrow{OQ}\) は向きが同じ.
\((b)\) \(\left|\overrightarrow{OP}\right|\left|\overrightarrow{OQ}\right|=1\).
以下の問いに答えよ.
(1) 点 \(P\) が \(O\) を除く \(C\) 上を動くとき,点 \(Q\) は \(\overrightarrow{OA}\) に直交する直線上を動くことを示せ.
(2) (1)の直線を \(l\) とする.\(l\) が \(C\) と \(2\) 点で交わるとき, \(r\) のとりうる値の範囲を求めよ.
反転(円に関する鏡像変換)
平面上において,\(O\) を中心とする半径 \(r\) の円を考える.
この円 \(O\) に関する反転とは,平面上の点 \(P\) に対して半直線 \(OP\) 上で,\(OP・OQ=r^2\) となる点 \(Q\) を対応させる対応のこと.

入試では頻出テーマの1つです。
差がつく問題になりますので,この問題を通して演習し経験値を身につけましょう!
解答・解説
(1)
 題意より
題意より
\(\left|\overrightarrow{OP}-\overrightarrow{OA}\right|=r\) ・・・①
\(\left|\overrightarrow{OA}\right|=r\) ・・・②
条件 \((a)\) より,正の実数 \(k\) を用いて
\(\overrightarrow{OQ}=k\overrightarrow{OP}\) ・・・③ とおける.
条件 \((b)\) より,\(\left|\overrightarrow{OP}\right|\left|k\overrightarrow{OP}\right|=1\)
よって,\(k=\displaystyle\frac{1}{\left|\overrightarrow{OP}\right|^2}\)
③より,\(\overrightarrow{OQ}=\displaystyle\frac{1}{\left|\overrightarrow{OP}\right|^2}\overrightarrow{OP}\) \(\iff\) \(\overrightarrow{OP}=\left|\overrightarrow{OP}\right|^2\overrightarrow{OQ}\) ・・・④
①を \(2\) 乗して
\(\left|\overrightarrow{OP}\right|^2-2\overrightarrow{OA}\cdot\overrightarrow{OP}+\left|\overrightarrow{OA}\right|^2=r^2\)
②より\(\left|\overrightarrow{OA}\right|^2=r^2\) であるから
\(\left|\overrightarrow{OP}\right|^2-2\overrightarrow{OA}\cdot\overrightarrow{OP}=0\)
これに④を代入すると,
\(\left|\overrightarrow{OP}\right|^4\left|\overrightarrow{OQ}\right|^2-2\left|\overrightarrow{OP}\right|^2\overrightarrow{OA}\cdot\overrightarrow{OQ}=0\)
\(\left|\overrightarrow{OP}\right|\not=0\) より
\(\left|\overrightarrow{OP}\right|^2\left|\overrightarrow{OQ}\right|^2-2\overrightarrow{OA}\cdot\overrightarrow{OQ}=0\)
条件 \((b)\) より
\(1-2\overrightarrow{OA}\cdot\overrightarrow{OQ}=0\)
よって,\(\overrightarrow{OA}\cdot\overrightarrow{OQ}=\displaystyle\frac{1}{2}\)
ここで,\(\overrightarrow{OA}=(a_{1},a_{2})\) , \(\overrightarrow{OQ}=(x,y)\) とおくと,
\(\overrightarrow{OA}\cdot\overrightarrow{OQ}=\displaystyle\frac{1}{2}\) \(\iff\) \(a_{1}x+a_{2}y=\displaystyle\frac{1}{2}\) となり,
これは直線 \(OA\) : \(a_{2}x-a_{1}y=0\) と直交する.
したがって題意は示された.
(2)
円の中心の点 \(A (a_{1},a_{2})\) と,直線 \(a_{1}x+a_{2}y=\displaystyle\frac{1}{2}\) の距離が \(r\) より小さくなれば良いので,
\(\displaystyle\frac{|a_{1}^2+a_{2}^2-\frac{1}{2}|}{\sqrt{a_{1}^2+a_{2}^2}}<r\)
②より \(a_{1}^2+a_{2}^2=r^2\) なので
\(\displaystyle\frac{|r^2-\frac{1}{2}|}{\sqrt{r^2}}<r\)
\(|r^2-\displaystyle\frac{1}{2}|<r^2\)
\(-r^2<r^2-\displaystyle\frac{1}{2}<r^2\)
\(r^2>\displaystyle\frac{1}{4}\)
\(r>0\) であるから,\(r>\displaystyle\frac{1}{2}\)







コメント