【2021早稲田大学・人間科学】線形計画法｜x^2+y^2,y/x,x+yの最大・最小

入試総合問題(三角関数の媒介変数・恒等式・線形計画法)

数学Ⅱの入試問題演習。答えだけでなく、考え方を重視。 三角関数の媒介変数の利用、kについての高等式・線形計画法を利用した問題。

mathmathmanabu.com

2021.12.04

解答・解説

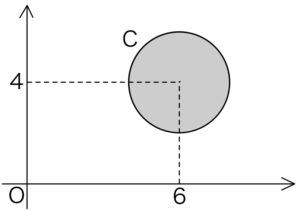円 \((x-6)^2+(y-4)^2=4\) を \(C\) とする．

不等式 \((x-6)^2+(y-4)^2≦4\) の表す領域は右の図の影付き部分である．

ただし，境界線を含む．

(１)　\(x^2+y^2\) の最大値

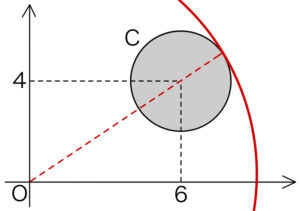\(x^2+y^2=r^2\) ・・・① とおく．

①は中心原点，半径 \(r\) の円を表す．

半径 \(r\) が最大となるのは，右図より

円①と円 \(C\) が内接するときであるから，

\(\sqrt{6^2+4^2}=r-2\)

よって，\(r=2\sqrt{13}+2\)

したがって，求める最大値は \(r^2=56+8\sqrt{13}\)

(２)　\(\displaystyle\frac{y}{x}\) の最小値

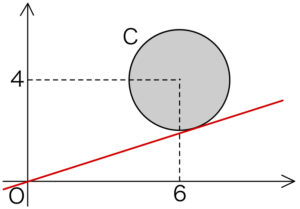\(\displaystyle\frac{y}{x}=k\) ・・・② とおく．

このとき \(y=kx\) は傾き \(k\) で原点を亨通る直線を表す．

直線②と円 \(C\) が共有点をもつ条件は，

円 \(C\) の中心 \((6,4)\) と直線②との距離が円 \(C\) の半径以下になるときであるから

\(\displaystyle\frac{|m\cdot 6+(-1)\cdot 4|}{\sqrt{k^2+(-1)^2}}≦2\)

\(|3m-2|≦\sqrt{k^2+1}\)

両辺を \(2\) 乗して式を整理すると

\(8k^2-12k+3≦0\)

よって，\(\displaystyle\frac{3-\sqrt{3}}{4}≦k≦\displaystyle\frac{3+\sqrt{3}}{4}\)

したがって，求める最小値は \(\displaystyle\frac{3-\sqrt{3}}{4}\)

(３)　\(x+y\) の最大値

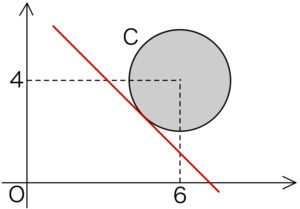\(x+y=p\) ・・・③ とおく．

③は傾き \(-1\) , \(y\) 切片 \(p\) の直線を表す．

直線③と円 \(C\) が共有点をもつための条件は，

円 \(C\) の中心 \((6,4)\) と直線③との距離が円 \(C\) の半径以下になるときであるから

\(\displaystyle\frac{|1\cdot 6+1\cdot 4-p|}{\sqrt{1^2+1^2}}≦2\)

\(|p-10|≦2\sqrt{2}\)

\(-2\sqrt{2}≦p-10≦2\sqrt{2}\)

\(-2\sqrt{2}+10≦p≦2\sqrt{2}+10\)

したがって求める最大値は，\(2\sqrt{2}+10\)