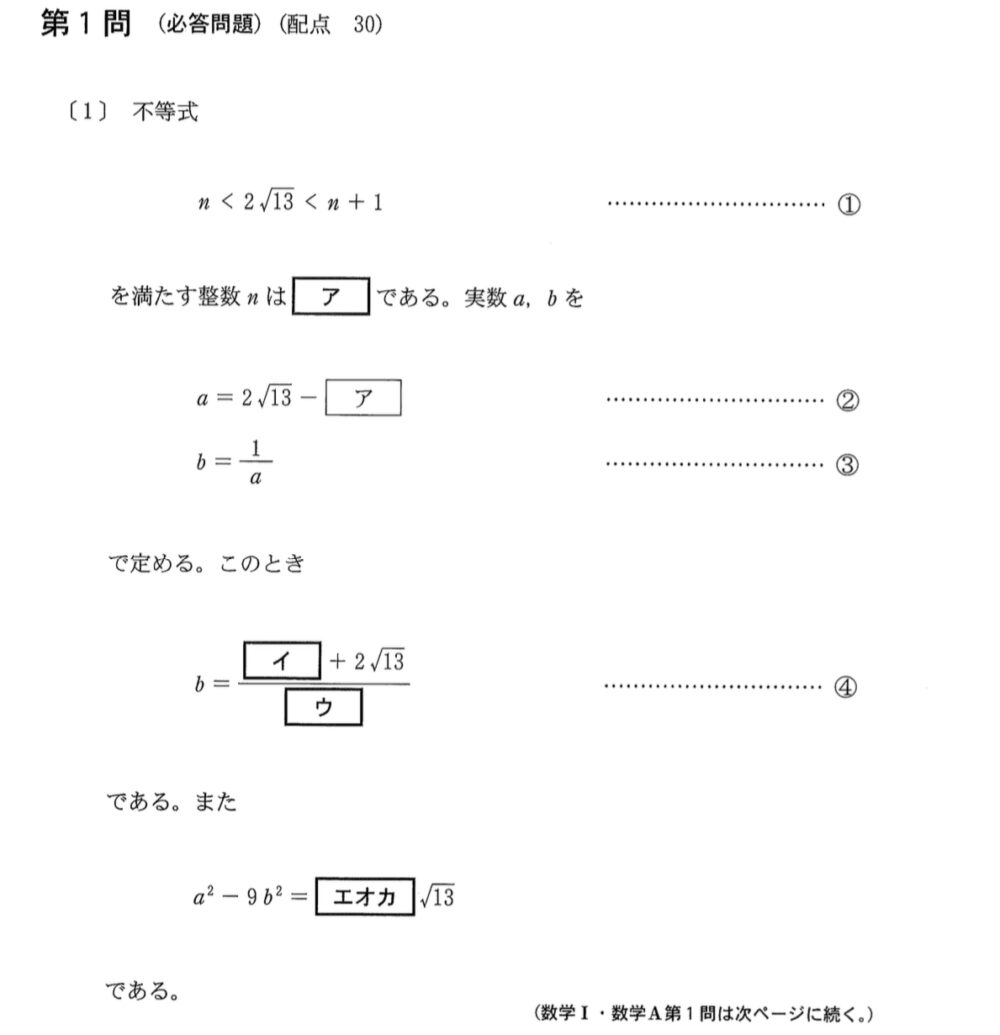
〔1〕問題《ア〜カ》
〔1〕解答・解説《ア~カ》
\(2\sqrt{13}=\sqrt{52}\) で,
\(49<52<64\) より \(7<\sqrt{52}<8\)
よって,\(7<2\sqrt{13}<8\) であるから,
\(n<2\sqrt{13}<n+1\) を満たす整数 \(n\) は \(7\) ・・・《ア》
\(a=2\sqrt{13}-7\) のとき
\(b=\displaystyle\frac{1}{a}=\displaystyle\frac{1}{2\sqrt{13}-7}\)
これを有理化すると
\(b=\displaystyle\frac{2\sqrt{13}+7}{(2\sqrt{13}-7)( 2\sqrt{13}+7)}=\)\(\displaystyle\frac{7+2\sqrt{13}}{3}\) ・・・《イウ》
また,\(a^2-9b^2=(a+3b)(a-3b)\) であり
《イウ》の結果から,\(3b=7+2\sqrt{13}\) なので
\(a^2-9b^2=\left\{(2\sqrt{13}-7)+( 7+2\sqrt{13})\right\}\left\{(2\sqrt{13}-7)-( 7+2\sqrt{13})\right\}=\)\(-56\sqrt{13}\) ・・・《エ~カ》
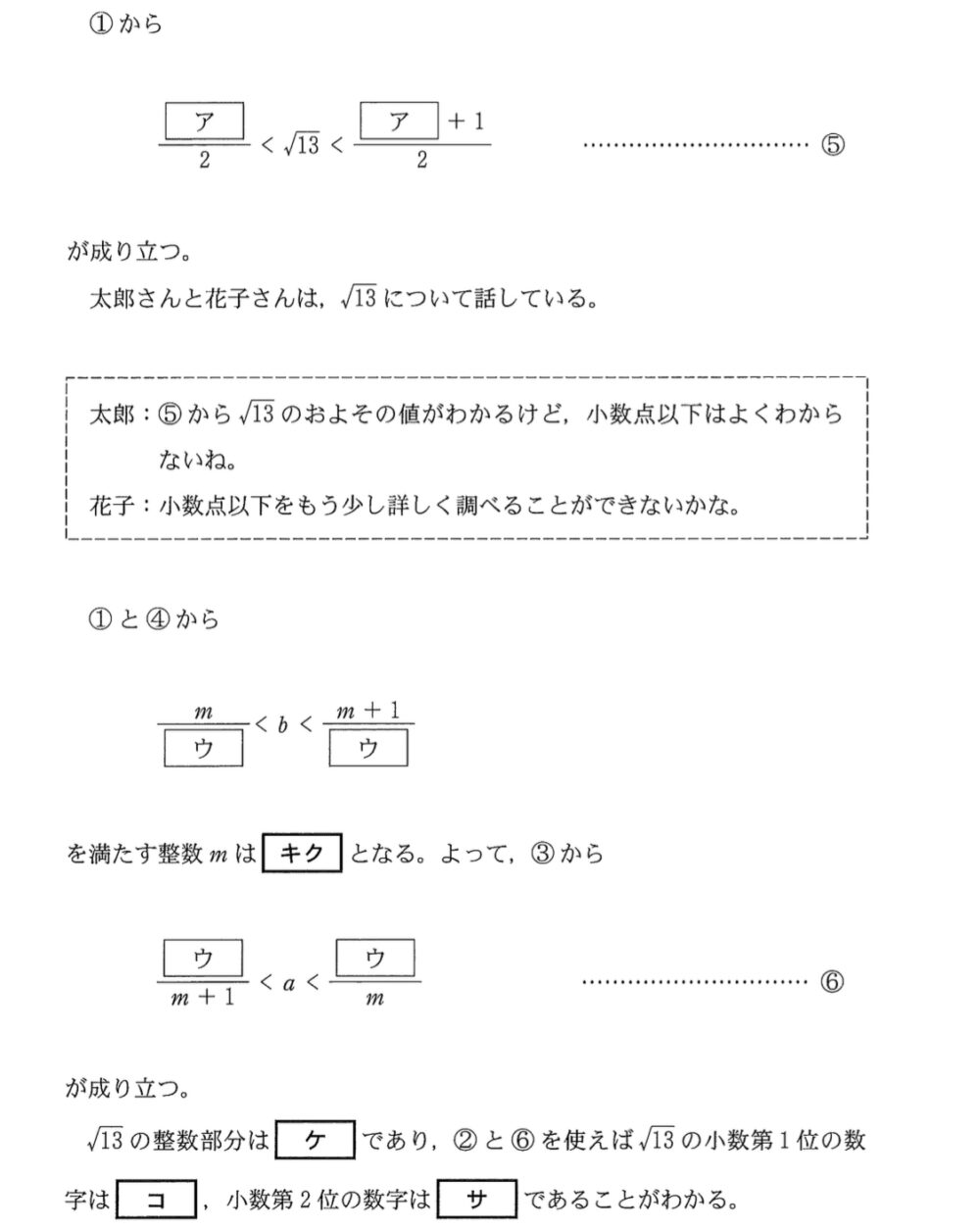
〔1〕問題《キ~サ》
〔1〕解答・解説《キ~サ》
①から \(\displaystyle\frac{7}{2}<\sqrt{13}<4\) ・・・⑤
①と④から
\(14<7+2\sqrt{13}<15\)
\(\displaystyle\frac{14}{3}<b<5\) より \(m=14\) ・・・《キク》
\(\displaystyle\frac{14}{3}<\displaystyle\frac{1}{a}<5\)
\(\displaystyle\frac{1}{5}<a<\displaystyle\frac{3}{14}\) ・・・⑥が成り立つ
また、
\(3<\sqrt{13}<4\) より \(\sqrt{13}\) の整数部分は \(3\) ・・・《ケ》
これから \(\sqrt{13}\) の小数部分は \(\sqrt{13}-3\)
ここで⑥の結果から
\(\displaystyle\frac{1}{5}<2\sqrt{13}-7<\displaystyle\frac{3}{14}\)
\(\displaystyle\frac{6}{5}<2\sqrt{13}-6<\displaystyle\frac{17}{14}\)
\(\displaystyle\frac{3}{5}<\sqrt{13}-3<\displaystyle\frac{17}{28}\)
\(0.60<\sqrt{13}-3<0.607\cdots\) より
\(\sqrt{13}\) の小数第1位の数字は \(6\),小数第2位の数字は \(0\) ・・・《コサ》








コメント