【2022旭川医科大学・医学部】倍数の個数、集合と場合の数

\(30\) 個の自然数なので，\(1\) つ \(1\) つ頑張って調べれば答えは求められますが・・・

ここでは \(30\) でなくもっと大きな値になった場合でも対応できるように解答を作成しましょう！

解答・解説

問１(１)　\(4\) の倍数または \(6\) の倍数

\(1\) から \(30\) までの自然数において，\(4\) の倍数の集合を \(A\)，\(6\) の倍数の集合を \(B\) とおく．

\(4\) の倍数の個数は \(30=4\times 7+2\) より \(n\left(A\right)=7\) 個

\(6\) の倍数の個数は \(30=6\times 5\) より \(n\left(B\right)=5\) 個

\(4\) の倍数かつ \(6\) の倍数，つまり \(12\) の倍数の個数は

\(30=12\times 2+6\) より \(n\left(A\cap B\right)=2\) 個

よって \(4\) の倍数または \(6\) の倍数は，\(n\left(A\cup B\right)=7+5-2=10\) 個

問１(２)　\(2\) の倍数であるが \(4\) でも \(6\) でも割り切れない数

\(1\) から \(30\) までの自然数において，\(2\) の倍数の集合を \(C\) とする．

\(2\) の倍数の個数は \(30=2\times 15\) より \(n\left(C\right)=15\) 個

\(2\) の倍数であるが \(4\) でも \(6\) でも割り切れない数は，\(C\cap\left(\overline{A}\cap\overline{B}\right)\) と表される．

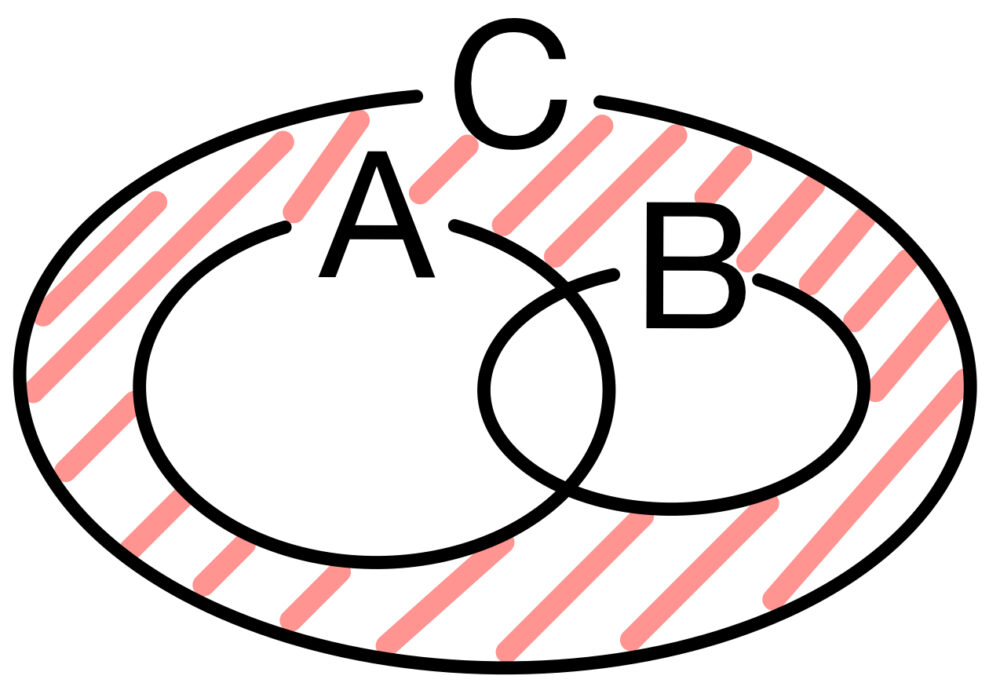ベン図を利用して考えると，

\(C\cap\left(\overline{A}\cap\overline{B}\right)=n\left(C\right)-n\left(A\cup B\right)\)

(１)の結果から，

\(C\cap\left(\overline{A}\cap\overline{B}\right)=15-10=5\) 個

問２(１)　少なくとも一方の数が \(12\) の倍数となる選び方

\(1\) から \(30\) までの自然数において，\(12\) の倍数は \(2\) 個ある．

\(30\) 個の自然数から互いに異なる \(2\) 数を選ぶとき，少なくとも一方の数が \(12\) の倍数であるのは，

余事象を考えて，

\(_{30}C_{2}-_{28}C_{2}=\displaystyle\frac{30\times 29}{2\times 1}-\displaystyle\frac{28\times 27}{2\times 1}=57\) 通り

問２(２)　\(2\) つの数の積が \(12\) の倍数となる選び方

( ⅰ )　少なくとも一方の数が \(12\) の倍数のとき

(１)より，\(57\) 通り

( ⅱ )　ともに \(12\) の倍数でないとき

(ア)　少なくとも一方の数が \(6\) の倍数のとき

\(1\) から \(30\) までの自然数のうち \(6\) の倍数であり，\(12\) の倍数でない数は，\(6\)，\(18\)，\(30\) の \(3\) 個ある．

・選んだ \(2\) 数が両方とも「\(6\)，\(18\)，\(30\)」のいずれかのとき

\(_{3}C_{2}=3\) 通り

・選んだ \(2\) 数の一方のみが「\(6\)，\(18\)，\(30\)」のいずれかとき

もう一方の数は \(6\) でない偶数であるから，\(3\times 10=30\) 通り

(イ)　選んだ \(2\) 数がいずれも \(6\) の倍数でないとき

このとき，一方が \(6\) の倍数でない \(3\) の倍数「\(3\)，\(9\)，\(15\)，\(21\)，\(27\)」のいずれかで，

もう一方が \(6\) の倍数でない \(4\) の倍数「\(4\)，\(8\)，\(16\)，\(20\)，\(28\)」のいずれか．

よって，\(5\times 5=25\) 通り

したがって，\(57+3+30+25=115\) 通り