【2022藤田医科大学(後期)】x>0において、x/2+2/x^2の最小値｜①数学Ⅲの微分②相加相乗の利用

相加平均・相乗平均の関係を利用した解法

考え方

\(\displaystyle\frac{x}{2}+\displaystyle\frac{2}{x^2}\) について

この式の形を見たときに、相加相乗は使えないか？？と一瞬頭をよぎることができましたか？？

相加相乗平均の関係については、

「相加平均・相乗平均の関係はいつ使う？使うタイミングの見抜き方（発展）」や

「３つの相加・相乗平均の関係｜実践問題【慶応義塾大学】」を参考にしてください。

しかし，与式にそのまま相加平均・相乗平均の関係を用いても，

\(\displaystyle\frac{x}{2}+\displaystyle\frac{2}{x^2}≧2\sqrt{\displaystyle\frac{x}{2}\cdot\displaystyle\frac{2}{x^2}}=2\sqrt{\displaystyle\frac{1}{x}}\)

となり，ルートの中に \(x\) が残ってしまう・・・

そこで，

解答・解説

\(x>0\) において

\(\displaystyle\frac{x}{2}+\displaystyle\frac{2}{x^2}=\displaystyle\frac{x}{4}+\displaystyle\frac{x}{4}+\displaystyle\frac{2}{x^2}\)

\(x>0\) であるから，相加平均・相乗平均の関係より

\(\displaystyle\frac{x}{4}+\displaystyle\frac{x}{4}+\displaystyle\frac{2}{x^2}≧3\sqrt[3]{\displaystyle\frac{x}{4}\cdot\displaystyle\frac{x}{4}\cdot\displaystyle\frac{2}{x^2}}=\displaystyle\frac{3}{2}\)

等号成立は，\(\displaystyle\frac{x}{4}\)\(\left(=\displaystyle\frac{x}{4}\right)\)\(=\displaystyle\frac{2}{x^2}\)

つまり，\(x^3=8\) で \(x>0\) より \(x=2\) のとき

したがって，\(x=2\) のとき最小値は \(\displaystyle\frac{3}{2}\)

【参考】数学Ⅲの微分を利用した解法

\(f(x)=\displaystyle\frac{x}{2}+\displaystyle\frac{2}{x^2}\) ( \(x>0\) )とおく

\(f^{\prime}(x)=\displaystyle\frac{1}{2}-\displaystyle\frac{4}{x^3}=\displaystyle\frac{x^3-8}{2x^3}\)

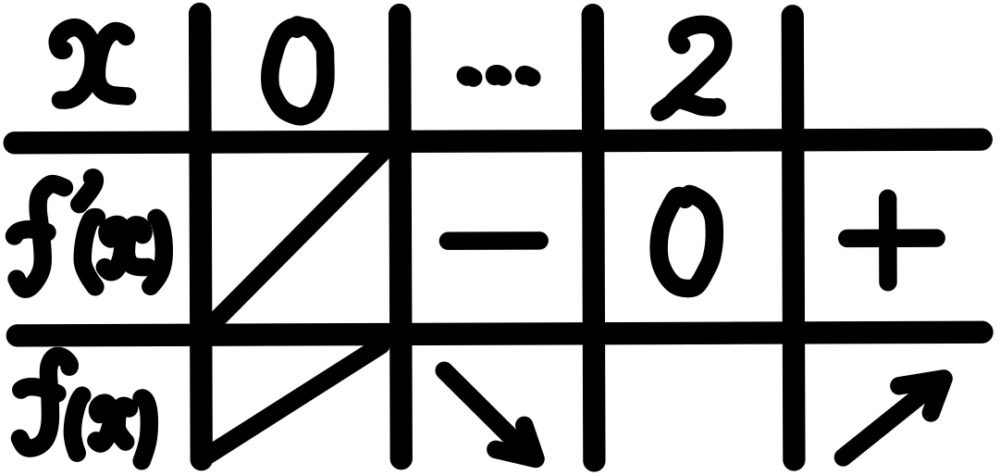
\(\displaystyle\lim_{x\rightarrow\infty}h(x)=\infty \)

\(x\rightarrow\infty\) のとき，関数 \(y=f(x)\) は，

\(y=\displaystyle\frac{x}{2}\) を漸近線として無限大に発散していく！