【2023神戸大学・理系・第5問】
媒介変数表示
\(x=\sin t\) ,\(y=\cos\left(t-\displaystyle\frac{\pi}{6}\right)\sin t\) ( \(0≦t≦\pi\) )
で表される曲線を \(C\) とする.以下の問に答えよ.
(1) \(\displaystyle\frac{dx}{dt}=0\) または \(\displaystyle\frac{dy}{dt}=0\) となる \(t\) の値を求めよ.
(2) \(C\) の概形を \(xy\) 平面上に描け.
(3) \(C\) の \(y≦0\) の部分と \(x\) 軸で囲まれた図形の面積を求めよ.
解答・解説
(1) \(\displaystyle\frac{dx}{dt}=0\),\(\displaystyle\frac{dy}{dt}=0\) となる \(t\) の値
\(x=\sin t\) より
\(\displaystyle\frac{dx}{dt}=\cos t=0\) のとき \(t=\displaystyle\frac{\pi}{2}\)
\(y=\cos\left(t-\displaystyle\frac{\pi}{6}\right)\sin t\) より
\(\displaystyle\frac{dy}{dt}=-\sin\left(t-\displaystyle\frac{\pi}{6}\right)\sin t+\cos\left(t-\displaystyle\frac{\pi}{6}\right)\cos t\)
\(=\cos\left\{t+\left(t-\displaystyle\frac{\pi}{6}\right)\right\}=\cos\left(2t-\displaystyle\frac{\pi}{6}\right)\)
\(-\displaystyle\frac{\pi}{6}≦2t-\displaystyle\frac{\pi}{6}≦\displaystyle\frac{11\pi}{6}\) より
\(\displaystyle\frac{dy}{dt}=0\) のとき
\(2t-\displaystyle\frac{\pi}{6}=\displaystyle\frac{\pi}{2},\displaystyle\frac{3\pi}{2}\)
\(t=\displaystyle\frac{\pi}{3},\displaystyle\frac{5\pi}{6}\)
したがって,\(t=\displaystyle\frac{\pi}{3},\displaystyle\frac{\pi}{2},\displaystyle\frac{5\pi}{6}\)
(2) \(C\) の概形を \(xy\) 平面上に描け.
(1)の結果から
| \(t\) | \(0\) | ・・・ | \(\displaystyle\frac{\pi}{3}\) | ・・・ | \(\displaystyle\frac{\pi}{2}\) | ・・・ | \(\displaystyle\frac{5\pi}{6}\) | ・・・ | \(\pi\) |
| \(\displaystyle\frac{dx}{dt}\) | + | + | + | \(0\) | ー | ー | ー | ||
| \(x\) | \(0\) | → | \(\displaystyle\frac{\sqrt{3}}{2}\) | → | \(1\) | ← | \(\displaystyle\frac{1}{2}\) | ← | \(0\) |
| \(\displaystyle\frac{dy}{dt}\) | + | \(0\) | ー | ー | ー | \(0\) | + | ||
| \(y\) | \(0\) | ↑ | \(\displaystyle\frac{3}{4}\) | ↓ | \(\displaystyle\frac{1}{2}\) | ↓ | \(-\displaystyle\frac{1}{4}\) | ↑ | \(0\) |
\(y=0\) \(\iff\) \(\cos\left(t-\displaystyle\frac{\pi}{6}\right)\sin t=0\)
\(0<t<\pi\) のとき \(\sin t>0\) より
\(\cos\left(t-\displaystyle\frac{\pi}{6}\right)=0\)
\(-\displaystyle\frac{\pi}{6}<t-\displaystyle\frac{\pi}{6}<\displaystyle\frac{5\pi}{6}\) なので
\(t-\displaystyle\frac{\pi}{6}=\displaystyle\frac{\pi}{2}\)
よって \(t=\displaystyle\frac{2\pi}{3}\) より,\(C\) は原点以外に \(x\) 軸と \(\left(\displaystyle\frac{\sqrt{3}}{2},0\right)\) を共有点にもつので,\(C\) のグラフは下図のようになる.
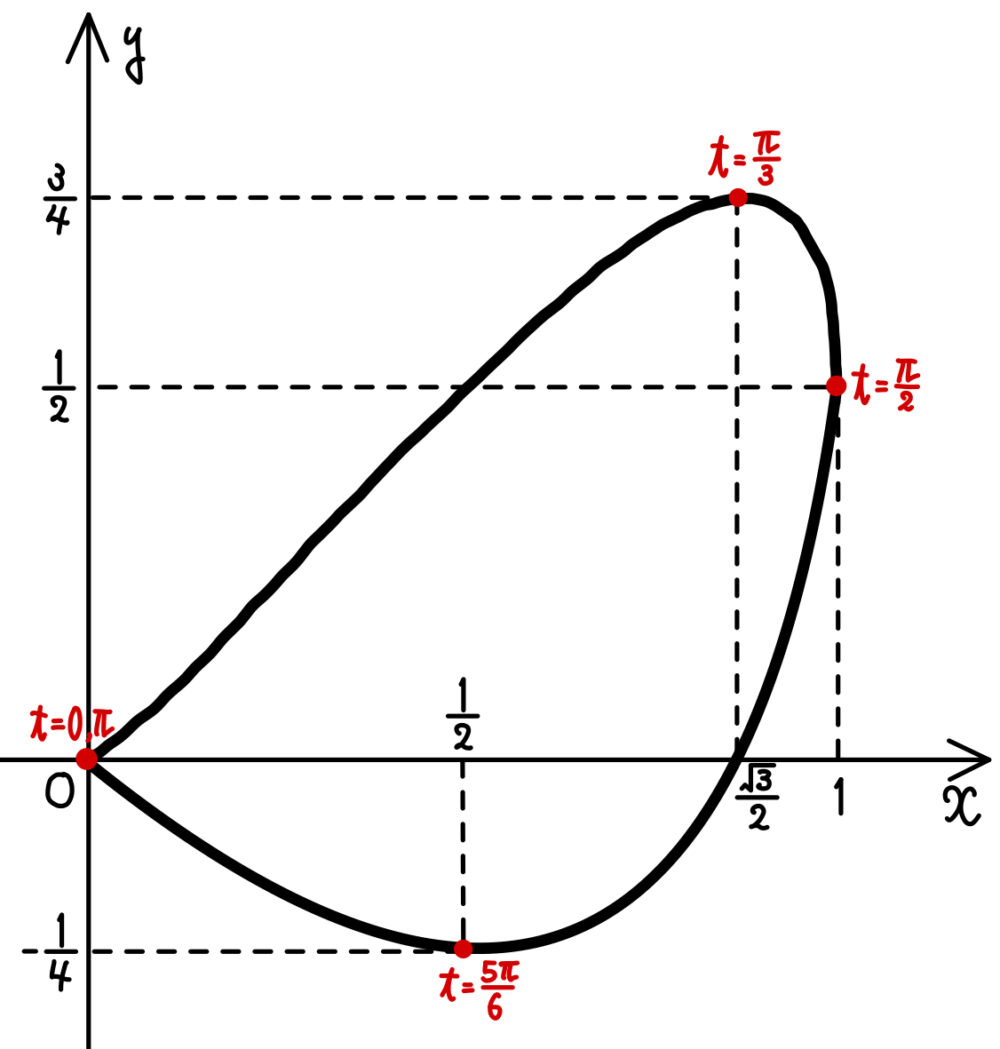
(3) \(C\) の \(y≦0\) の部分と \(x\) 軸で囲まれた図形の面積
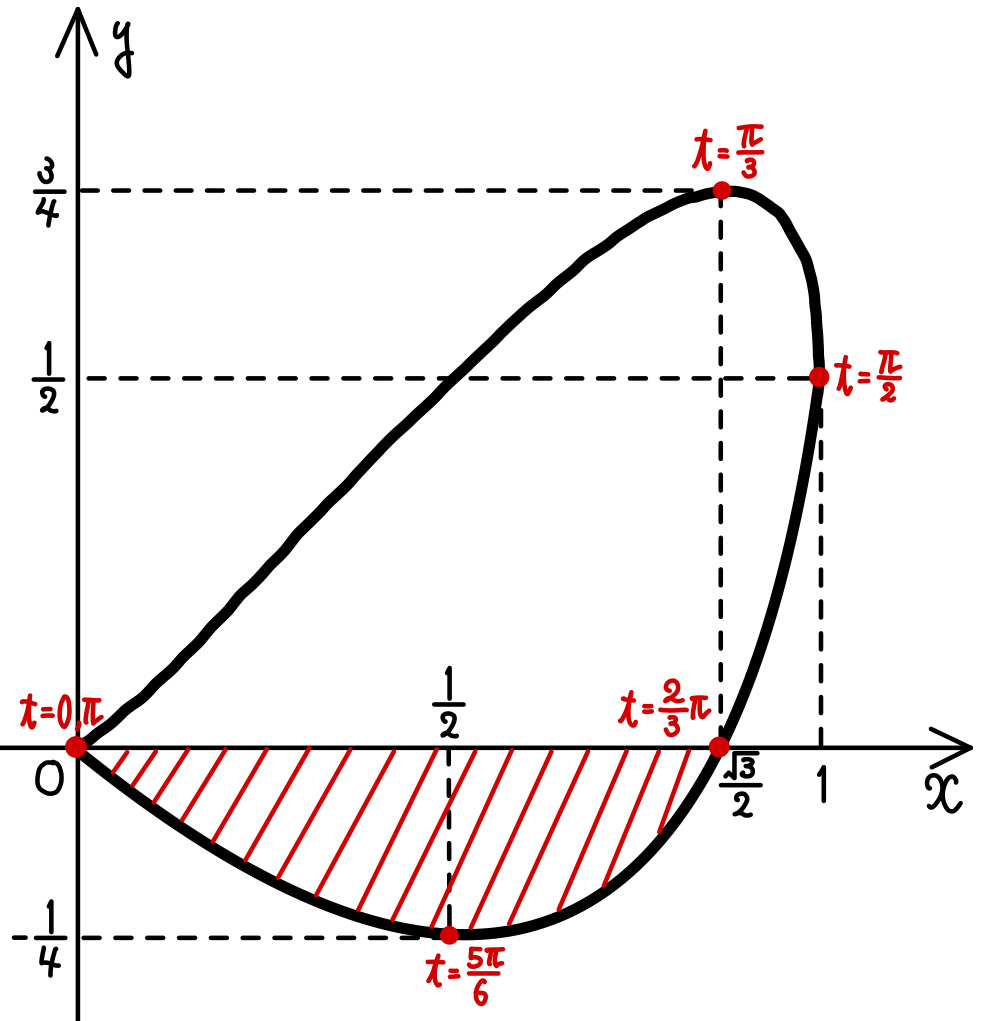
求める面積を \(S\) とすると(1),(2)より
\(S=\displaystyle\int^{\frac{\sqrt{3}}{2}}_{0}(-y)dx\)
\(=\displaystyle\int^{\frac{2\pi}{3}}_{\pi}(-y)\displaystyle\frac{dx}{dt} dt\)
\(=\displaystyle\int^{\pi}_{\frac{2\pi}{3}} \cos\left(t-\displaystyle\frac{\pi}{6}\right)\sin t\cos t dt\)
\(=\displaystyle\int^{\pi}_{\frac{2\pi}{3}} \left(\displaystyle\frac{\sqrt{3}}{2}\cos t+\displaystyle\frac{1}{2}\sin t\right)\sin t\cos t dt\)
\(=\displaystyle\int^{\pi}_{\frac{2\pi}{3}} \left(\displaystyle\frac{\sqrt{3}}{2}\sin t\cos^2 t+\displaystyle\frac{1}{2}\sin^2 t\cos t\right) dt\)
\(=\Bigl[-\displaystyle\frac{\sqrt{3}}{6}\cos^3 t+\displaystyle\frac{1}{6}\sin^3t\Bigr]^{\pi}_{\frac{2\pi}{3}}\)
\(=\displaystyle\frac{\sqrt{3}}{12}\)







コメント