【2022藤田医科大学(前期)】
\(3\) 個のサイコロを同時に投げるとき，出た目の積が \(8\) で割り切れる確率を求めよ．
今年度実施された、藤田医科大学の小問の１つの確率の問題です．
１度はどこかで類題を見たことがある、定期考査にも出題さそうな、基本的な問題です．
医学部志望となると、どうしても難しい問題ばかりに目がいきがちですが、こういった基礎的な問題をしっかりとこなせるかどうかが凄く大切です．
考え方
\(8\) の倍数を考えるにあたり、\(2\) を約数に持つかどうか、また持つとしたら何個約数に持つのかを考え、次の \(3\) つのグループに分け考えていく．
・奇数(1、3、5) [ \(2\) を約数に持たない]
・2、6 [ \(2\) を \(1\) つ約数に持つ]
・4 [ \(2\) を \(2\) つ約数に持つ]
解答
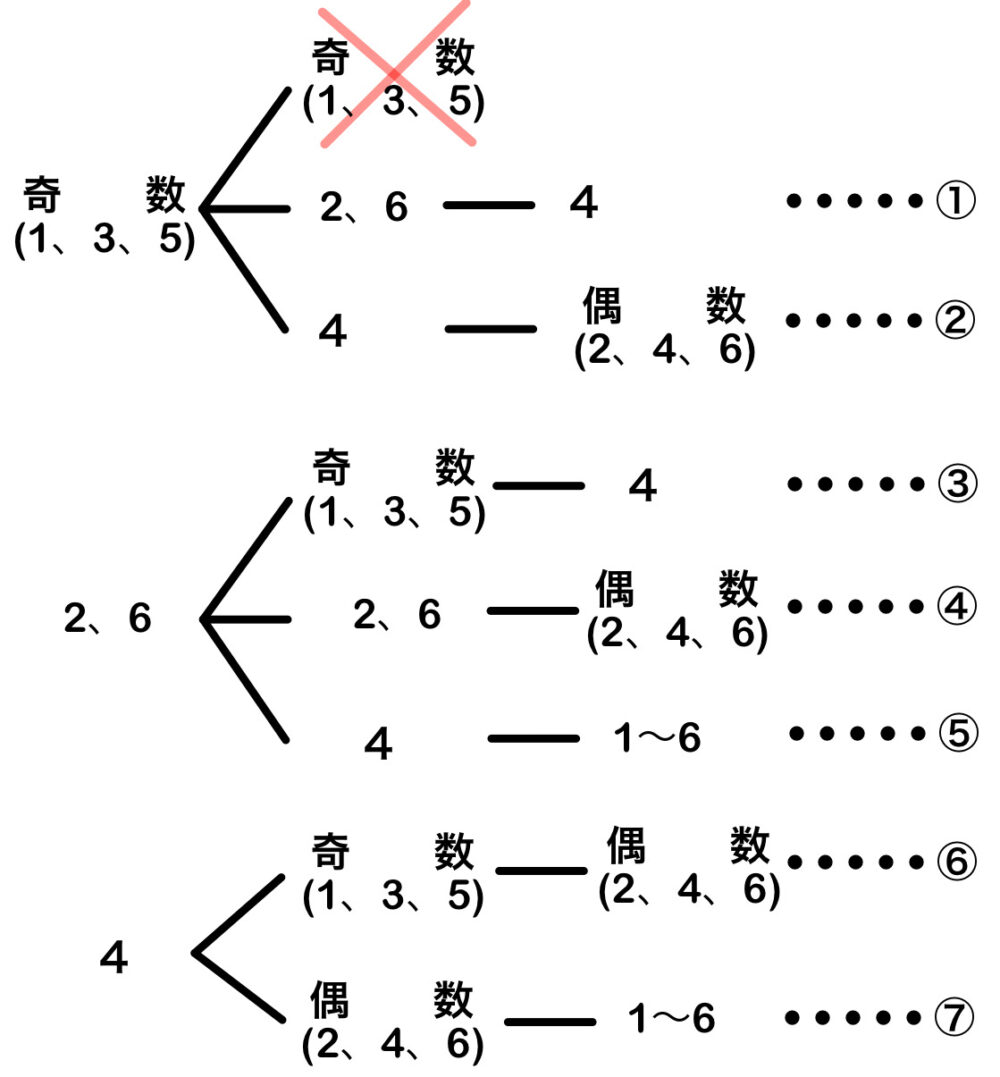
上図のように、初めのさいころがどのグループになるかで場合分けをして、樹形図を考えた．
①：\(3\times2\times1=6\) 通り
②：\(3\times1\times3=9\) 通り
③：\(2\times3\times1=6\) 通り
④：\(2\times2\times3=12\) 通り
⑤：\(2\times1\times6=12\) 通り
⑥：\(1\times3\times3=9\) 通り
⑦：\(1\times3\times6=18\) 通り
①～⑦より \(72\) 通り．
したがって求める確率は、\(\displaystyle\frac{72}{6^3}=\displaystyle\frac{1}{3}\)
確率の有名問題も一緒に勉強しましょう！
【数学A】確率Pnの最大値の求め方・考え方（2018関西学院大学）
受験数学での頻出・重要テーマの、反復試行の確率の最大値の求め方。
ただ答えを求めるだけでなく、考え方について解説。
mathmathmanabu.com
2021.08.28
2017 京都大学の類題｜さいころ・確率・最大値と最小値の差
場合の数・確率は、原則として正攻法または余事象で考える．
どのようなときに正攻法、余事象を利用するのかについても言及．また、本問では両方の解法をそれぞれ紹介．
mathmathmanabu.com
2021.12.13
n 人ジャンケン「あいこ」の確率【一般化】
正攻法と余事象の２通りの解法。一般化の考え方、二項定理や部屋分け問題の有名問題を組み合わせてん人のじゃんけんのあいこの確率を考える。
mathmathmanabu.com
2021.08.26
コメント