【2021九州大学・理】
座標空間内の \(4\) 点 \(O(0,0,0)\) , \(A(1,0,0)\) , \(B(0,1,0)\) , \(C(0,0,2)\) を考える．以下の問に答えよ．
(１) 四面体 \(OABC\) に内接する球の中心の座標を求めよ．
(２) 中心の \(x\) 座標，\(y\) 座標，\(z\) 座標がすべて正の実数であり，\(xy\) 平面，\(yz\) 平面，\(zx\) 平面のすべてと接する球を考える．この球が平面 \(ABC\) と交わるとき，その交わりとしてできる円の面積の最大値を求めよ．
考え方・方針
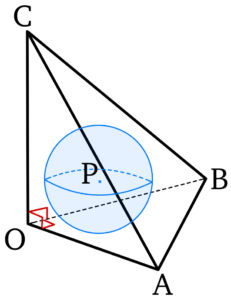求める球の中心を \(P\) とおき，球の半径を \(r\) ( \(>0\) ) とおく
(１) \(xy\) 平面，\(yz\) 平面，\(zx\) 平面のすべてと接する球であるから，
\(P (r,r,r)\) と表すことができる．
四面体 \(OABC\) に内接するとき，点 \(P\) から平面 \(ABC\) への距離が \(r\) と等しくなれば良い！
平面の方程式の公式と，点と面の距離の公式を活用することで処理することができる！
平面の方程式
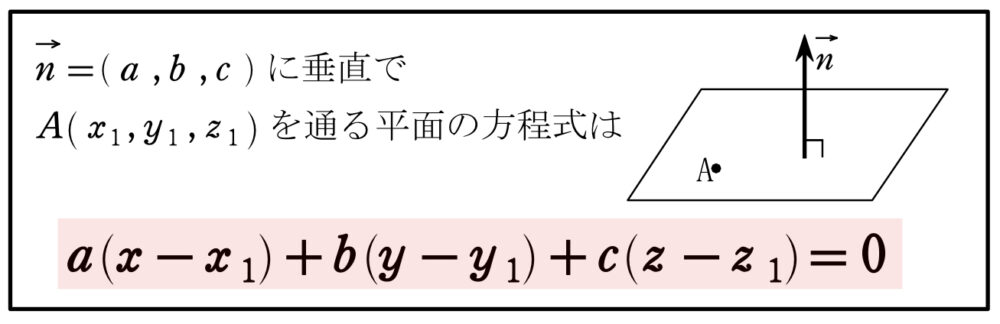
公式の証明や使い方などについては、「平面の方程式・点と平面の距離・空間上の直線の方程式・外積の公式まとめ・例題演習」を参考にしてください！
参考（\(x\)切片，\(y\)切片，\(z\)切片を通る平面の方程式）
本問では \(A(1,0,0)\) , \(B(0,1,0)\) , \(C(0,0,2)\) を通る平面 \(ABC\) の方程式だからすぐにわかるね！
点と平面の距離の公式・証明
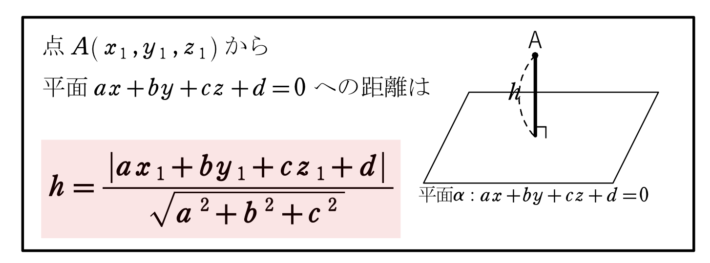
解答・解説
【2021九州大学・理】
座標空間内の \(4\) 点 \(O(0,0,0)\) , \(A(1,0,0)\) , \(B(0,1,0)\) , \(C(0,0,2)\) を考える．以下の問に答えよ．
(１) 四面体 \(OABC\) に内接する球の中心の座標を求めよ．
(２) 中心の \(x\) 座標，\(y\) 座標，\(z\) 座標がすべて正の実数であり，\(xy\) 平面，\(yz\) 平面，\(zx\) 平面のすべてと接する球を考える．この球が平面 \(ABC\) と交わるとき，その交わりとしてできる円の面積の最大値を求めよ．
(１)
四面体 \(OABC\) に内接する球の中心を \(P\) , 半径を \(r\) ( \(r>0\) ) とおく．
この球は，\(xy\) 平面，\(yz\) 平面，\(zx\) 平面のすべてと接するから
\(P(r,r,r)\) とおくことができる．
次に，\(3\) 点 \(A(1,0,0)\) , \(B(0,1,0)\) , \(C(0,0,2)\) を通る平面の方程式は，
\(\displaystyle\frac{x}{1}+\displaystyle\frac{y}{1}+\displaystyle\frac{z}{2}=1\)
\(\iff\) \(2x+2y+z-2=0\) ・・・①
球の中心点 \(P\) から，平面①までの距離を \(h\) とおくと，
題意の条件を満たすのは，\(h=r\) のとき．
よって
\(h=\displaystyle\frac{|2r+2r+r-2|}{\sqrt{2^2+2^2+1^2}}=r\)
\(|5r-2|=3r\)
\(2\) 乗すると
\((5r-2)^2=9r^2\)
式を整理してまとめると，
\((4r-1)(r-1)=0\)
よって， \(r=\displaystyle\frac{1}{4}\), \(1\)
ここで，\(r=1\) のとき \(P(1,1,1)\) は四面体 \(OABC\) の外部にあるため不適．
したがって求める球の中心は \(P\left(\displaystyle\frac{1}{4} , \displaystyle\frac{1}{4} ,\displaystyle\frac{1}{4}\right)\)
(２)
(１)の結果を利用すると，\(h<r\) を満たせば良い
よって，\(h=\displaystyle\frac{|5r-2|}{3}<r\)
両辺正であるから \(2\) 乗しても不等号の向きは変わらないので
\((5r-2)^2<9r^2\)
\((4r-1)(r-1)<0\)
\(\displaystyle\frac{1}{4}<r<1\) ・・・②
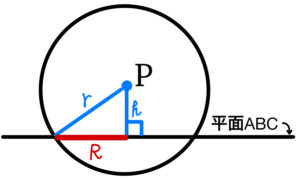
このとき，球 \(P\) と平面が \(ABC\) が交わってできる円の半径を \(R\) とおくと
\(R^2=r^2-h^2=r^2-\left(\displaystyle\frac{|5r-2|}{3}\right)^2\)
よって，\(R=-\displaystyle\frac{16}{9}\left(r-\displaystyle\frac{5}{8}\right)^2+\displaystyle\frac{1}{4}\)
となるから，②の範囲における \(R^2\) の最大値は
\(r=\displaystyle\frac{5}{8}\) のとき \(\displaystyle\frac{1}{4}\)
したがって，求める円の面積の最大値は，\(\displaystyle\frac{\pi}{4}\)
コメント