【2022佐賀大学・医学部・第4問】
複素数 \(z\) について,\(1\),\(z\),\(z^2\) を表す複素数平面上の点をそれぞれ \(A\),\(B\),\(C\) とする.次の問に答えよ.
(1) 点 \(A\),\(B\),\(C\) が正三角形の \(3\) つの頂点となる \(z\) をすべて求めよ.
(2) 点 \(A\),\(B\),\(C\) が直角三角形の \(3\) つの頂点となる点 \(z\) 全体を図示せよ.

(1)考え方・解答・解説
一般の点を中心とする回転
点 \(\alpha\) を中心に、点 \(\beta\) を \(k\) 倍して、角 \(\theta\) だけ回転した点が \(\gamma\) のとき
\(\gamma-\alpha=k(\cos \theta+i \sin \theta) (\beta-\alpha)\)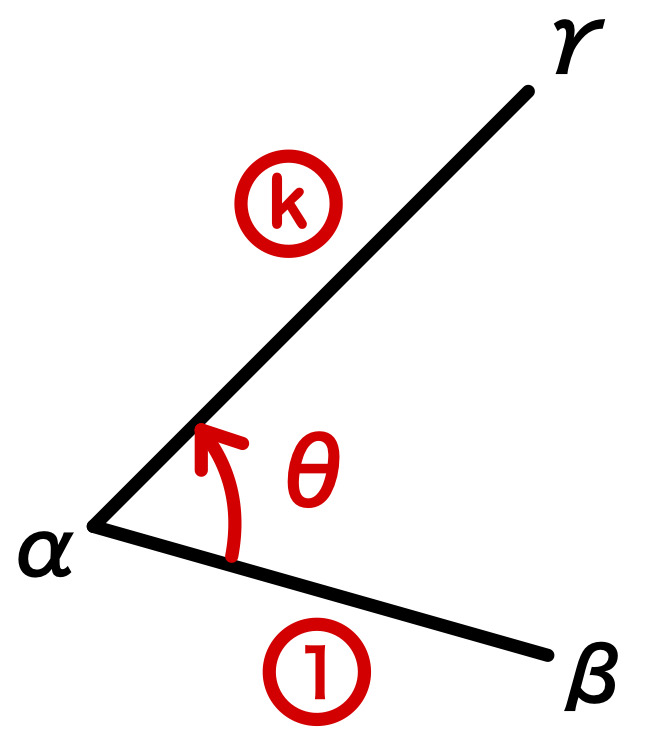
または
\(\displaystyle\frac{\gamma-\alpha}{\beta-\alpha}=k(\cos \theta+i \sin \theta)\)
(1) 点 \(A\),\(B\),\(C\) が正三角形の \(3\) つの頂点となる \(z\)
\(3\) 点 \(A\),\(B\),\(C\) が正三角形となるとき,\(3\) 点はすべて異なるので
\(\begin{cases}1\not=z\\z\not=z^2\\z^2\not=1\end{cases}\) \(\iff\) \(z\not=0,\pm1\) ・・・①
このとき,点 \(A\) を中心として,\(B\) を \(\pm\displaystyle\frac{\pi}{3}\) 回転させた点が \(C\) となればよいので,
\(\displaystyle\frac{z^2-1}{z-1}=\cos\left(\pm\displaystyle\frac{\pi}{3}\right)+i\sin\left(\pm\displaystyle\frac{\pi}{3}\right)\) (複号同順)
\(z+1=\displaystyle\frac{1}{2}\pm\displaystyle\frac{\sqrt{3}}{2}i\)
よって,\(z=-\displaystyle\frac{1}{2}\pm\displaystyle\frac{\sqrt{3}}{2}i\)
(2)考え方・解答・解説


\(\theta=90°\) のとき,
\(\displaystyle\frac{\gamma-\alpha}{\beta-\alpha}=k(\cos 90°+i \sin 90°)=ki\)
となり純虚数となります!
実数・純虚数となる条件
・\(z\) が実数 \(\iff\) \(\overline{ z } = z\)
・\(z\) が純虚数 \(\iff\) \(\overline{ z } = -z\)、\(z\not=0\)
(2) 点 \(A\),\(B\),\(C\) が直角三角形の \(3\) つの頂点となる点 \(z\)
( ⅰ ) \(\angle BAC=90°\) のとき
\(\displaystyle\frac{z^2-1}{z-1}=z+1\) が純虚数となるので
\(z+1+\overline{(z+1)}=0\)
よって,\(z+\overline{z}=2\)
\(x\),\(y\) を実数として \(z=x+yi\) とおくと
\(2x=-2\) \(\iff\) \(x=-1\)
( ⅱ ) \(\angle ABC=90°\) のとき
\(\displaystyle\frac{z^2-z}{1-z}=-z\) が純虚数となるので
\(-z+\overline{(-z)}=0\)
よって,\(z+\overline{z}=0\)
\(x\),\(y\) を実数として \(z=x+yi\) とおくと
\(2x=0\) \(\iff\) \(x=0\)
( ⅲ ) \(\angle ACB=90°\) のとき
\(\displaystyle\frac{z-z^2}{1-z^2}=\displaystyle\frac{z}{1+z}\) が純虚数となるので
\(\displaystyle\frac{z}{1+z}+\overline{\left(\displaystyle\frac{z}{1+z}\right)}=0\)
\(z(1+\overline{z})+\overline{z}(1+z)=0\)
\(z\overline{z}+\displaystyle\frac{1}{2}z+\displaystyle\frac{1}{2}\overline{z}=0\)
\(\left(z+\displaystyle\frac{1}{2}\right)\left(\overline{z}+\displaystyle\frac{1}{2}\right)=\displaystyle\frac{1}{4}\)
\(\left(z+\displaystyle\frac{1}{2}\right)\overline{\left(z+\displaystyle\frac{1}{2}\right)}=\displaystyle\frac{1}{4}\)
\(\left|z+\displaystyle\frac{1}{2}\right|^2=\displaystyle\frac{1}{4}\)
\(\left|z+\displaystyle\frac{1}{2}\right|=\displaystyle\frac{1}{2}\) となり
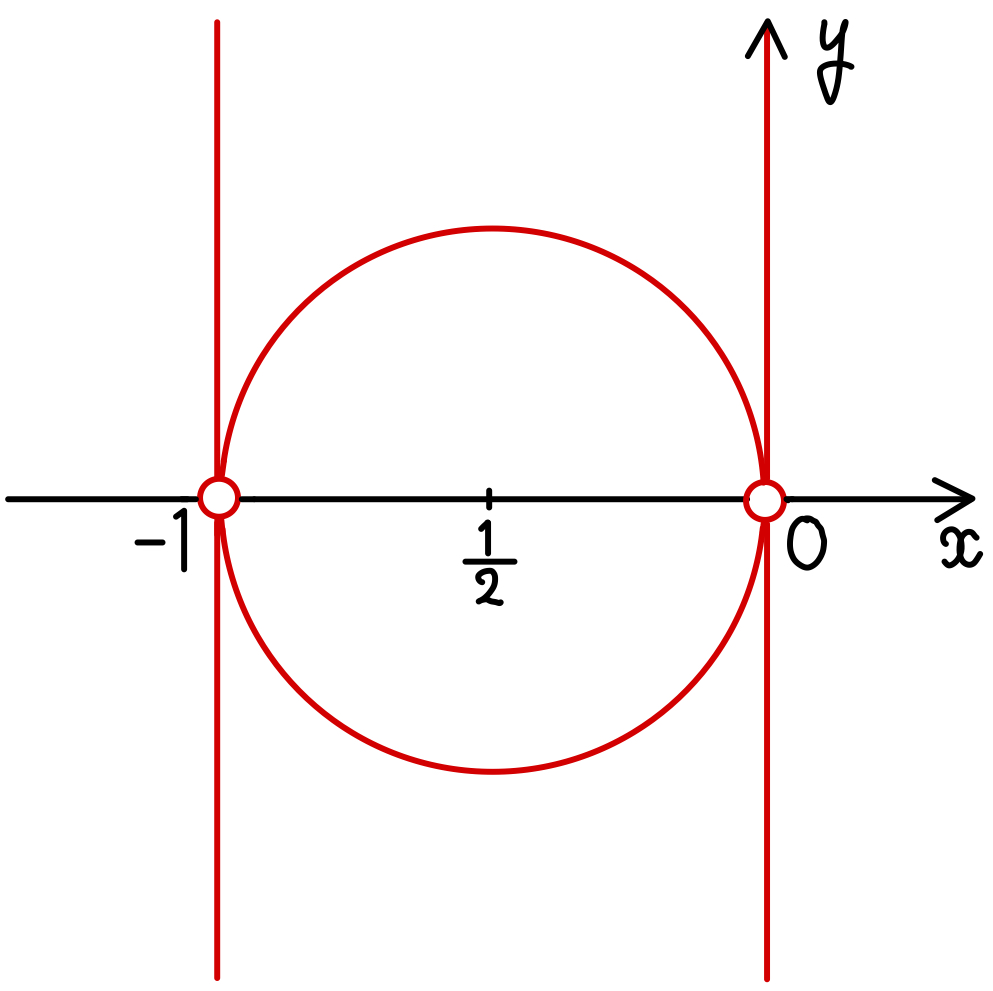
これは点 \(\left(-\displaystyle\frac{1}{2}\right)\) を中心とする半径 \(\displaystyle\frac{1}{2}\) の円
( ⅰ )〜( ⅲ )と(1)の①より
求める点 \(z\) の全体は数の赤線部分となる.
ただし,原点,点( \(-1\) ) を除く.







コメント