【2021数学ⅠA(第1日程)】第３問(場合の数と確率)

(１)問題と解答・解説《ア〜ウ》

(１)解答・解説《ア〜ウ》

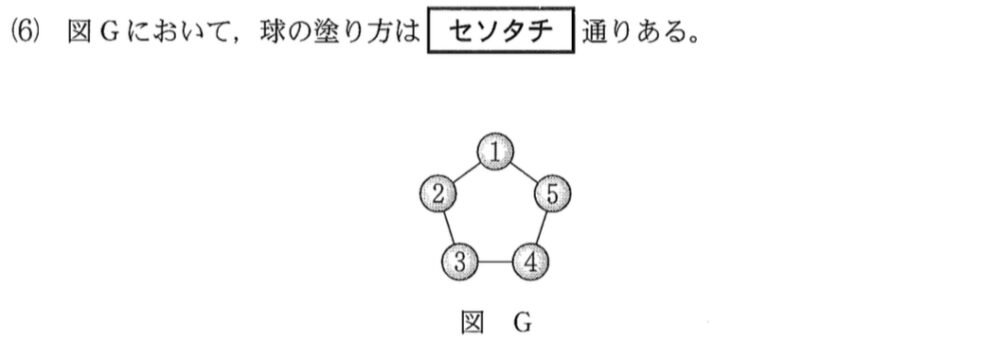
球 \(1\) の塗り方は，\(5\) 通りあり，

球 \(2\) の塗り方は，球 \(1\) の色以外の \(4\) 通り

球 \(3\) の塗り方は，球 \(2\) の色以外の \(4\) 通り

球 \(4\) の塗り方は，球 \(3\) の色以外の \(4\) 通り

球 \(5\) の塗り方は，球 \(4\) の色以外の \(4\) 通り

よって，\(5\times 4\times 4\times 4=\)\(320\) 通り・・・《アイウ》

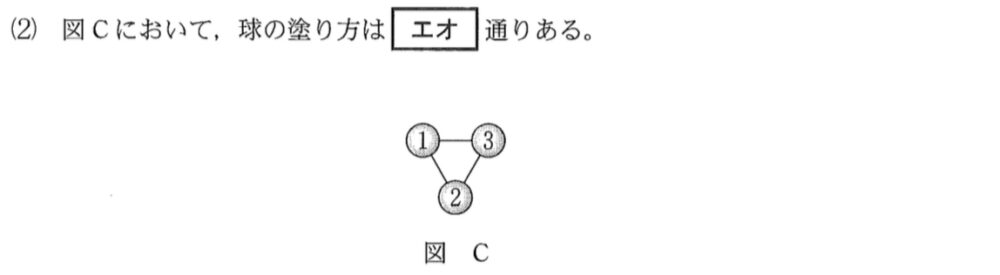
(２)問題と解答・解説《エオ》

(２)解答・解説《エオ》

球 \(1\) の塗り方は，\(5\) 通りあり，

球 \(2\) の塗り方は，球 \(1\) の色以外の \(4\) 通り

球 \(3\) の塗り方は，球 \(1\)，\(2\) の色以外の \(3\) 通り

よって，\(5\times 4\times 3=\)\(60\) 通り・・・《エオ》

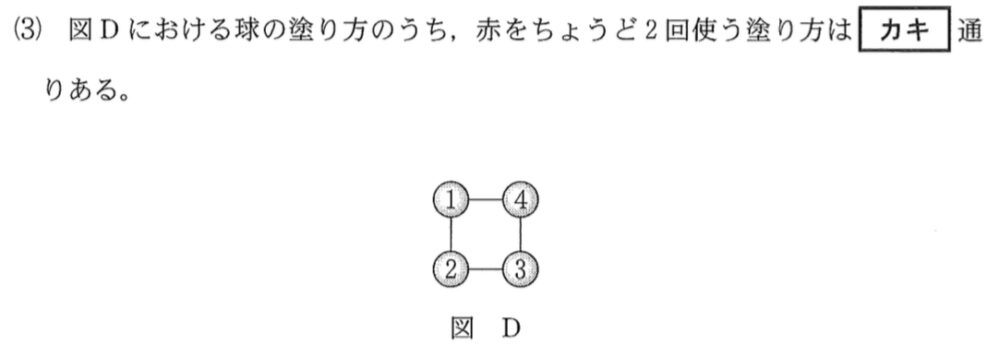
(３)問題と解答・解説《カキ》

(３)解答・解説《カキ》

図 \(D\) において，赤をちょうど \(2\) 回使う塗り方は，

( ⅰ )　球 \(1\) と球 \(3\) に赤を塗る　または　( ⅱ )　球 \(2\) と球 \(4\) に赤を塗る

のいずれかである．

( ⅰ )　球 \(1\) と球 \(3\) に赤を塗るとき

球 \(2\)，\(4\) の塗り方はそれぞれ，赤以外の \(4\) 通り

よって，\(4\times 4=16\) 通り

( ⅱ )　球 \(2\) と球 \(4\) に赤を塗るとき

球 \(1\)，\(3\) の塗り方はそれぞれ，赤以外の \(4\) 通り

よって，\(4\times 4=16\) 通り

したがって，\(16+16=\)\(32\) 通り・・・《カキ》

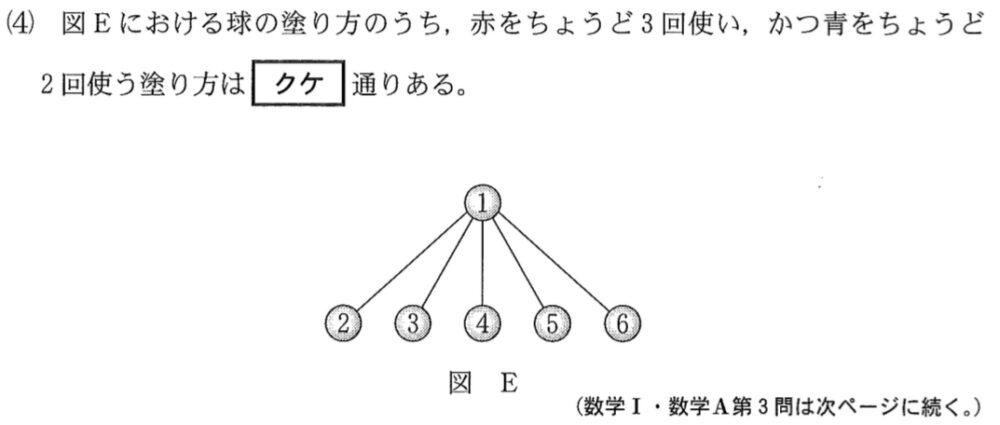
(４)問題と解答・解説《クケ》

(４)解答・解説《クケ》

図 \(E\) において，赤をちょうど \(3\) 回，青をちょうど \(2\) 回使う塗り方をするとき，

球 \(1\) は赤，青以外の \(3\) 色のいずれかで塗ればよい．

このとき，球 \(2\)〜 \(6\) の \(5\) 個の塗り方は，赤を \(3\) 回，青を \(2\) 回使用して塗ればよいので

\(_{5}C_{3}\times _{2}C_{2}=10\) 通り

よって，\(3\times 10=\)\(30\) 通り・・・《クケ》

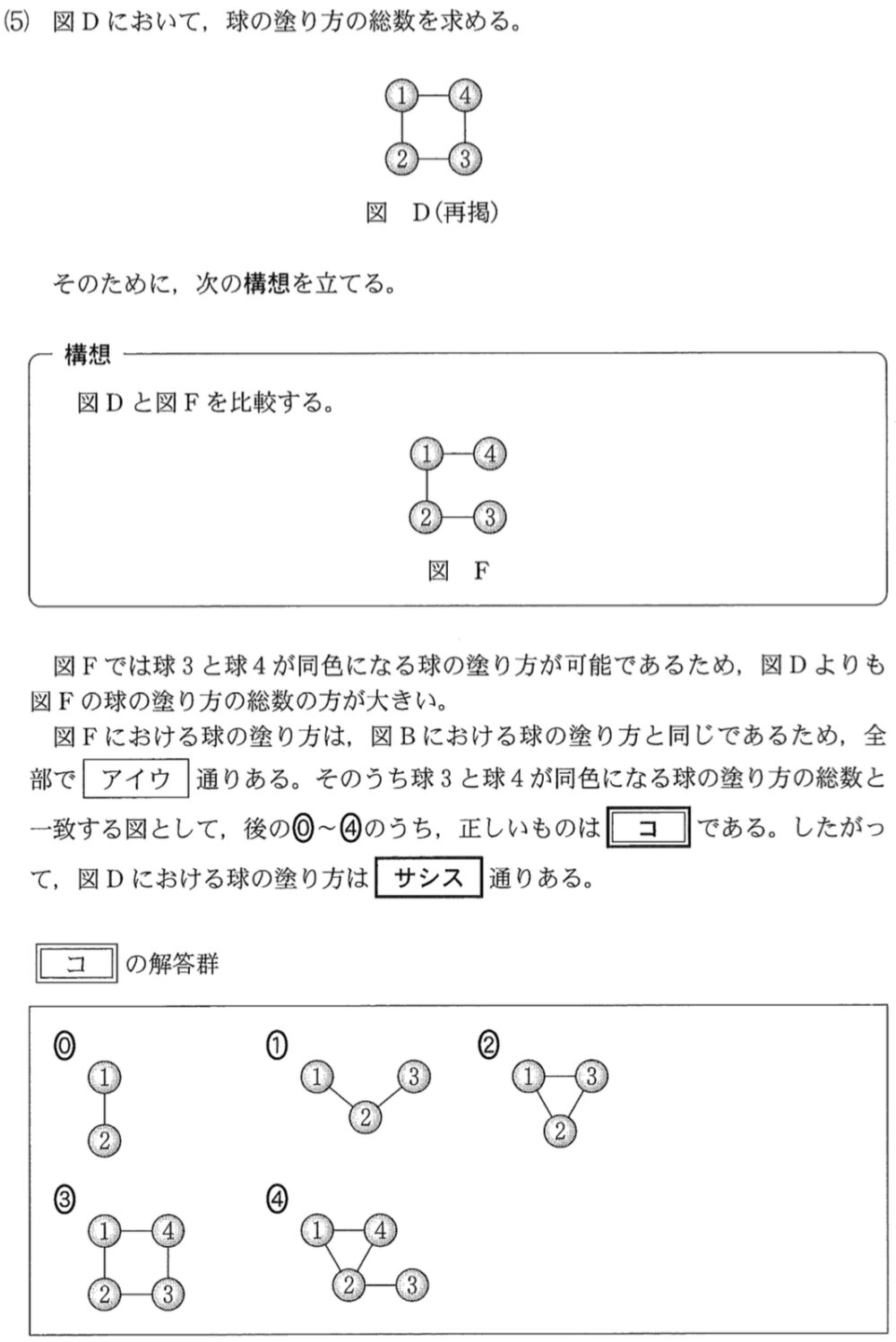
(５)問題と解答・解説《コ〜ス》

(５)解答・解説《コ〜ス》

図 \(F\) の塗り方は，(１)の図 \(B\) の塗り方と同じであるので，\(320\) 通りある．

その中で，球 \(3\) と球 \(4\) が同色になる塗り方は，球 \(3\) と球 \(4\) が一致する図として考えると，

図 \(C\) ・・・《コ：②》 と考えることができる．

よって(２)の結果から，\(60\) 通り

したがって図 \(D\) の球の塗り方は

\(320-60=\)\(260\) 通り・・・《サ〜ス》

(６)問題と解答・解説《セ〜チ》

(６)解答・解説《セ〜チ》

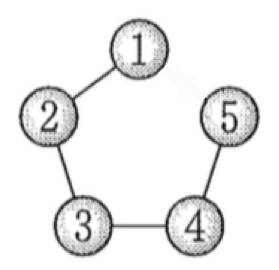(５)と同様に考える．

まず右図(球 \(1\) と球 \(5\) の間のひもを無くした形)の塗り方は

(１)と同様に考え，

\(5\times 4\times 4\times 4\times 4=1280\) 通り

この中で球 \(1\) と球 \(5\) が同色となる球の塗り方は(５)の結果から \(260\) 通り．

したがって求める塗り方は，

\(1280-260=\)\(1020\) 通り・・・《セ〜チ》