【2023立命館大学・全学統一方式・理系・第3問】

曲線の長さについて
媒介変数された曲線の長さ
曲線 \(x=f(t)\) , \(y=g(t)\) ( \(\alpha≦t≦\beta\) ) の長さ \(L\) は
\(L=\displaystyle\int^{\beta}_{\alpha}\sqrt{\left(\displaystyle\frac{dx}{dt}\right)^2+\left(\displaystyle\frac{dy}{dt}\right)^2} dt=\displaystyle\int^{\beta}_{\alpha}\sqrt{\left\{f^{\prime}(t)\right\}^2+\left\{g^{\prime}(t)\right\}^2} dt\)
曲線の方程式が媒介変数 \(t\) を用いて \(x=f(t)\) , \(y=g(t)\) ( \(\alpha≦t≦\beta\) ) と表され,\(f(t)\) , \(g(t)\) の導関数はともに連続であるとき,この曲線の長さ \(L\) について
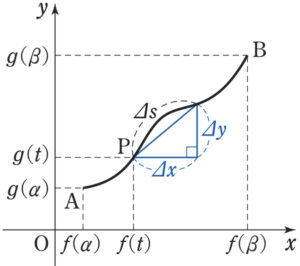 \(A (f(\alpha) , g(\alpha))\) ,\(B (f(\beta) , g(\beta))\) とする.
\(A (f(\alpha) , g(\alpha))\) ,\(B (f(\beta) , g(\beta))\) とする.
点 \(A\) から \(P (f(t) , g(t))\) までの曲線の長さを \(t\) の関数として考え,\(s(t)\) と表す.
また,\(t\) の増分 \(Δt\) に対する \(s(t)\) , \(f(t)\) , \(g(t)\) の増分をそれぞれ \(Δs\) , \(Δx\) , \(Δy\) とし, \(|Δt|\) が十分に小さいとき
\(|Δs| ≒ \sqrt{\left(Δx\right)^2+\left(Δy\right)^2}\) ・・・① と考えられる.
①より,\(\displaystyle\frac{Δs}{Δt} ≒ \sqrt{\left(\displaystyle\frac{Δx}{Δt}\right)^2+\left(\displaystyle\frac{Δy}{Δt}\right)^2}\) ・・・②
\(Δt \rightarrow 0\) のとき②より
\(\displaystyle\frac{ds}{dt}=\sqrt{\left\{f^{\prime}(t)\right\}^2+\left\{g^{\prime}(t)\right\}^2}\)
よって,\(s(t)\) は \(t\) の関数 \(\sqrt{\left\{f^{\prime}(t)\right\}^2+\left\{g^{\prime}(t)\right\}^2}\) の不定積分の \(1\) つであるから
\(\displaystyle\int^{\beta}_{\alpha}\sqrt{\left\{f^{\prime}(t)\right\}^2+\left\{g^{\prime}(t)\right\}^2} dt=s(\beta)-s(\alpha)\)
ここで,\(s(\alpha)=0\) , \(s(\beta)=L\) であるから
\(L=\displaystyle\int^{\beta}_{\alpha}\sqrt{\left\{f^{\prime}(t)\right\}^2+\left\{g^{\prime}(t)\right\}^2} dt\)
曲線 \(y=f(x)\) の長さ
曲線 \(y=f(x)\) ( \(a≦x≦b\) ) の長さ \(L\) は
\(L=\displaystyle\int^{b}_{a}\sqrt{1+\left(\displaystyle\frac{dy}{dx}\right)^2} dx=\displaystyle\int^{b}_{a}\sqrt{1+\left\{f^{\prime}(x)\right\}^2} dx\)
曲線 \(x=t\) , \(y=g(t)\) と考えると,
\(\displaystyle\frac{dx}{dt}=1\) , \(\displaystyle\frac{dy}{dt}=\displaystyle\frac{dy}{dx}\cdot\displaystyle\frac{dx}{dt}=\displaystyle\frac{dy}{dx}=f^{\prime}(x)\)
となるので,上で求めた
\(L=\displaystyle\int^{\beta}_{\alpha}\sqrt{\left(\displaystyle\frac{dx}{dt}\right)^2+\left(\displaystyle\frac{dy}{dt}\right)^2} dt=\displaystyle\int^{\beta}_{\alpha}\sqrt{\left\{f^{\prime}(t)\right\}^2+\left\{g^{\prime}(t)\right\}^2} dt\)
に代入すると得られる.

解答・解説
[1]
\(f^{\prime}(t)=\displaystyle\frac{1+\displaystyle\frac{2t}{2\sqrt{t^2+1}}}{t+\sqrt{t^2+1}}=\displaystyle\frac{1}{\sqrt{t^2+1}}\)
\(g^{\prime}(t)=\sqrt{t^2+1}+t\cdot\displaystyle\frac{2t}{2\sqrt{t^2+1}}+\displaystyle\frac{1}{\sqrt{t^2+1}}=2\sqrt{t^2+1}\)
[2]
曲線 \(C\) 上の点を \(P\left(\cos^4\theta,\sin^4\theta\right)\) とおくと
\(OP=\sqrt{\cos^8\theta+\sin^8\theta}\)
\(=\sqrt{\left(\displaystyle\frac{1+\cos 2\theta}{2}\right)^4+\left(\displaystyle\frac{1-\cos 2\theta}{2}\right)^4}\)
\(=\sqrt{\displaystyle\frac{1+6\cos^22\theta+\cos^42\theta}{8}}\)
\(=\displaystyle\frac{1}{2\sqrt{2}}\sqrt{(\cos^22\theta+3)^2-8}\)
\(0≦\theta≦\displaystyle\frac{\pi}{2}\) のとき \(0≦\cos^22\theta≦1\) より
\(\cos^22\theta=0\) \(\iff\) \(\theta=\displaystyle\frac{\pi}{4}\) のとき
\(OP\) は最小となる.よってその時の \((x,y)\) の座標は,\(\left(\displaystyle\frac{1}{4},\displaystyle\frac{1}{4}\right)\)
次に,
\(\displaystyle\frac{dx}{d \theta}=4\cos^3 \theta\cdot(-\sin \theta)=-4\sin \theta\cos^3\theta\)
\(\displaystyle\frac{dy}{d \theta}=4\sin^3 \theta\cos\theta\)
\(L=\displaystyle\int^{\frac{\pi}{2}}_{0}\sqrt{\left(\displaystyle\frac{dx}{d\theta}\right)^2+\left(\displaystyle\frac{dy}{d\theta}\right)^2} d \theta\) より
\(L=\displaystyle\int^{\frac{\pi}{2}}_{0}\sqrt{(-4\sin \theta\cos^3\theta)^2+(4\sin^3 \theta\cos\theta)^2}d \theta\)
\(=4\displaystyle\int^{\frac{\pi}{2}}_{0}\sin \theta\cos \theta\sqrt{\cos^4 \theta+\sin^4 \theta}d \theta\)
\(s=\sin^2 \theta\) とおくと
\(\displaystyle\frac{ds}{d \theta}=2\sin \theta\cos \theta\) ,
\(\cos^4 \theta+\sin^4 \theta=(\cos^2 \theta+\sin^2 \theta)^2-2\cos^2 \theta\sin^2 \theta\)
\(=1-2(1-\sin^2 \theta)\sin^2 \theta\)
\(=2s^2-2s+1\)
であり,\( \theta\) が \(0\) \(\rightarrow\) \(\displaystyle\frac{\pi}{2}\) のとき \(s\) は \(0\) \(\rightarrow\) \(1\) より
\(L=4\displaystyle\int^{1}_{0}\sqrt{2s^2-2s+1}\cdot\displaystyle\frac{1}{2} ds\)
\(=2\displaystyle\int^{1}_{0}\sqrt{2s^2-2s+1}ds\)
ここで,\(2s^2-2s+1=\displaystyle\frac{1}{2}\left\{(2s-1)^2+1\right\}\) より
\(L=\sqrt{2}\displaystyle\int^{1}_{0}\sqrt{(2s-1)^2+1} ds\)
\(2s-1=t\) とおくと
\(2ds=dt\) で
\(s\) が \(0\) \(\rightarrow\) \(1\) のとき \(t\) は \(-1\) \(\rightarrow\) \(1\) より
\(L=\sqrt{2}\displaystyle\int^{1}_{-1} \sqrt{t^2+1}\cdot\displaystyle\frac{1}{2}dt\)
\(\sqrt{t^2+1}\) は偶関数より
\(L=\sqrt{2}\displaystyle\int^{1}_{0}\sqrt{t^2+1}dt\)
[1]の結果から
\(L=\sqrt{2}\Bigl[\displaystyle\frac{1}{2}g(t)\Bigr]^{1}_{0}\)
\(=\displaystyle\frac{\sqrt{2}}{2}\left(g(1)-g(0)\right)\)
\(=1+\displaystyle\frac{\sqrt{2}}{2}\log{(1+\sqrt{2})}\)








コメント