【2022数学ⅡB】第４問(数列)
問題と解答・解説《ア〜ウ》
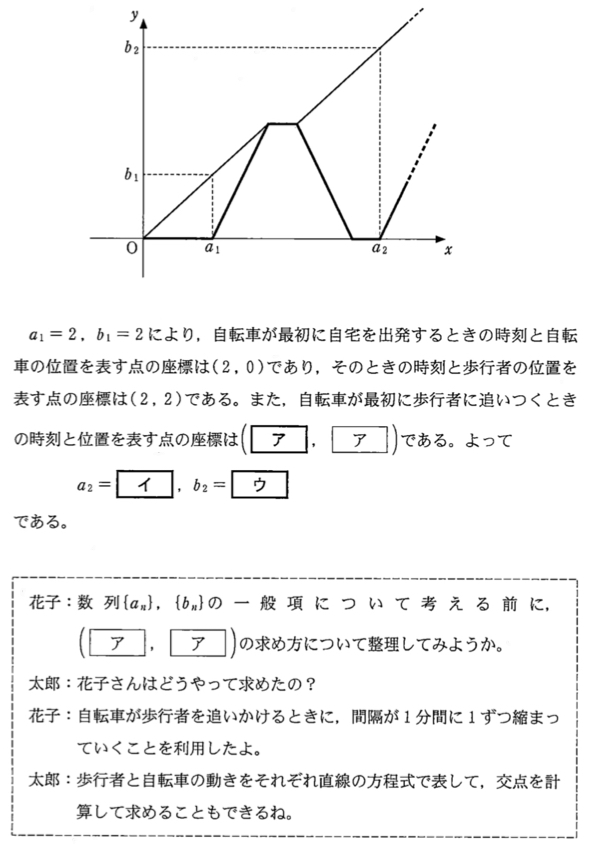
解答・解説《ア〜ウ》
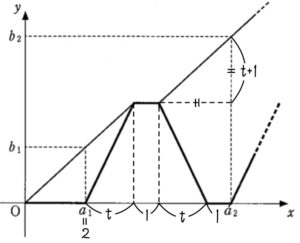自転車の移動の速さは毎分 \(2\) であるから，出発してから最初に歩行者に追いつくまでの時間を \(t\) とすると，自宅から \(2t\) の位置で追いつく．
歩行者は毎分 \(1\) の速さで歩くので
\(2+t=2t\) \(\iff\) \(t=2\)
よって，最初に歩行者に追いつく時刻と位置を表す点の座標は \((4,4)\) ・・・《ア》
次に，自転車と歩行者の位置関係を表すグラフから，
\(a_{2}=a_{1}+t+1+t+1=8\) ・・・《イ》
\(b_{2}=4+(t+1)=7\) ・・・《ウ》
問題と解答・解説《エオ》
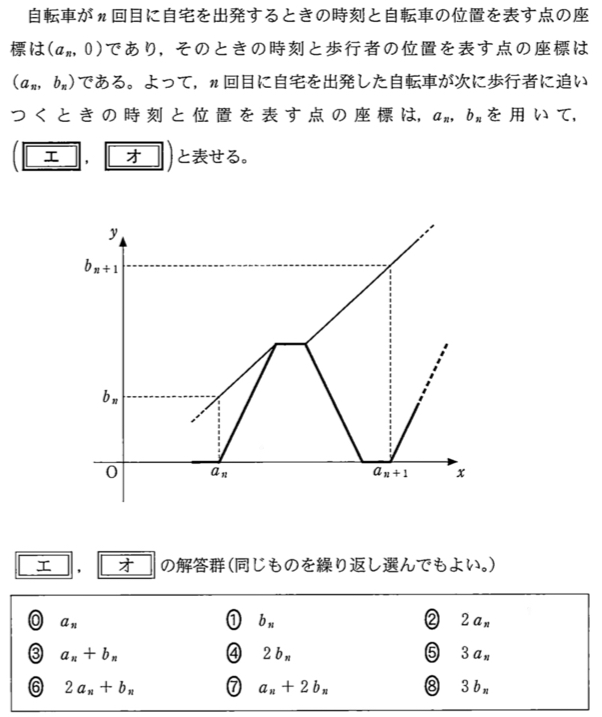
解答・解説《エオ》
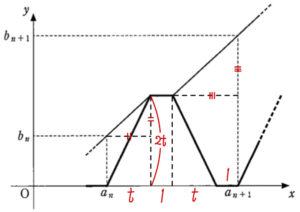
自転車が \(n\) 回目に自宅を出発してから次に歩行者に追いつくまでの時間を \(t\) とする．
上と同様に考えて，右のグラフより
\(b_{n}+t=2t\) \(\iff\) \(t=b_{n}\)
よって追いつく時刻は，
\(a_{n}+t=a_{n}+b_{n}\)
であり，そのときの位置は
\(2t=2b_{n}\)
したがって，\((a_{n}+b_{n},2b_{n})\) ・・・《エ：③，オ：④》
問題と解答・解説《カ〜セ》
解答・解説《カ〜セ》
(先程の続き)
右図より
\(a_{n+1}=a_{n}+t+1+t+1=a_{n}+2t+2\)
\(t=b_{n}\) より
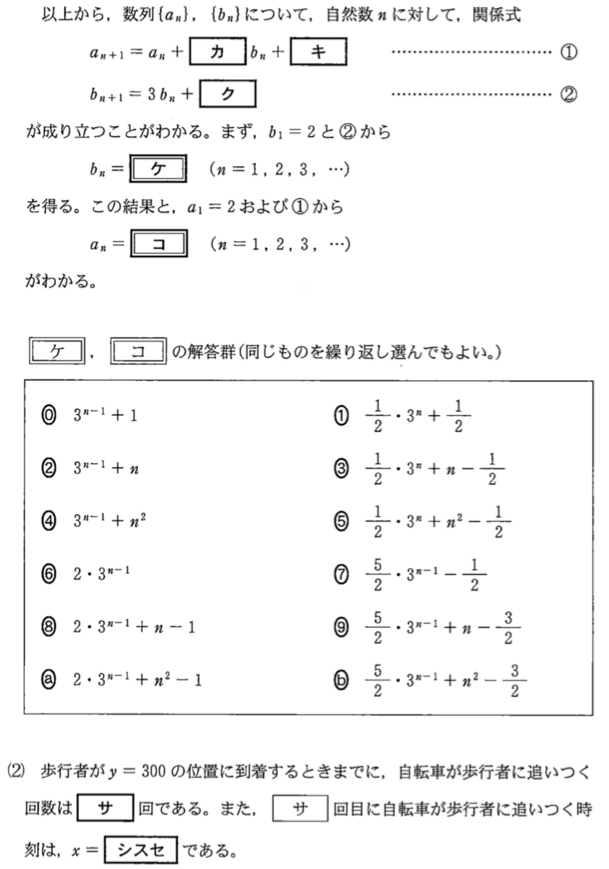
\(a_{n+1}=a_{n}+2b_{n}+2\) ・・・《カキ》
また，\(b_{n+1}=b_{n}+t+(t+1)=b_{n}+2t+1\)
\(b_{n+1}=3b_{n}+1\) ・・・《ク》
が成り立つ．
\(b_{1}=2\) , \(b_{n+1}=3b_{n}+1\) より
\(b_{n+1}=3b_{n}+1\) \(\iff\) \(b_{n+1}+\displaystyle\frac{1}{2}=3\left(b_{n}+\displaystyle\frac{1}{2}\right)\) より
数列 \(\left\{b_{n}+\displaystyle\frac{1}{2}\right\}\) は，初項が \(b_{1}+\displaystyle\frac{1}{2}=\displaystyle\frac{5}{2}\) ，公比が \(3\) の等比数列であるから
\(b_{n}+\displaystyle\frac{1}{2}=\displaystyle\frac{5}{2}\cdot3^{n-1}\)
よって，\(b_{n}=\displaystyle\frac{5}{2}\cdot3^{n-1}-\displaystyle\frac{1}{2}\) ・・・《ケ：⑦》
また，\(a_{n+1}=a_{n}+2b_{n}+2\) より
\(a_{n+1}=a_{n}+2\left(\displaystyle\frac{5}{2}\cdot3^{n-1}-\displaystyle\frac{1}{2}\right)+2\)
\(a_{n+1}=a_{n}+5\cdot3^{n-1}+1\)
\(n≧2\) のとき
\(a_{n}=a_{1}+\displaystyle\sum_{k=1}^{n-1}{(5\cdot3^{k-1}+1)}\) であるから
\(a_{n}=2+\displaystyle\frac{5(3^{n-1}-1)}{3-1}+n-1=\displaystyle\frac{5}{2}\cdot3^{n-1}+n-\displaystyle\frac{3}{2}\)
\(n=1\) のとき \(a_{1}=2\) となり成り立つ．
したがって，\(a_{n}=\displaystyle\frac{5}{2}\cdot3^{n-1}+n-\displaystyle\frac{3}{2}\) ・・・《コ：⑨》
(２) \(y=300\) の位置に歩行者が到着するまでに自転車が歩行者に追いつく回数 \(n\) は
\(2b_{n}≦300\) をみたす最大の \(n\) である．
\(2\left(\displaystyle\frac{5}{2}\cdot3^{n-1}-\displaystyle\frac{1}{2}\right)≦300\)
\(\iff\) \(3^{n-1}≦60.2\)
これを満たす最大の整数 \(n\) は \(n=4\) であるから， \(4\) 回 ・・・《サ》
このとき，自転車が歩行者に追いつく時刻 \(x\) は
\(x=a_{4}+b_{4}=\left(\displaystyle\frac{5}{2}\cdot3^3+4-\displaystyle\frac{3}{2}\right)+\left(\displaystyle\frac{5}{2}\cdot3^3-\displaystyle\frac{1}{2}\right)=\)\(137\) ・・・《シスせ》
コメント