因数分解の手順
- 共通因数でくくる(分母も!)
- 公式の利用
- 最低次数の文字に注目
手順1:共通因数でくくる(分母も!)

共通因数 \(xy\) だけでなく、分母もくくろう!
【解答】
\(\displaystyle\frac{1}{2}x^2y-\displaystyle\frac{1}{3}xy^2=\displaystyle\frac{1}{6}xy(3x-2y)\)
手順2:因数分解の公式一覧
- \(x^2+(a+b)x+ab=(x+a)(x+b)\)
- \(a^2+2ab+b^2=(a+b)^2\)
- \(a^2-2ab+b^2=(a-b)^2\)
- \(a^2-b^2=(a+b)(a-b)\)
- \(acx^2+(ad+bc)x+bd=(ax+b)(cx+d)\) [たすきがけ]
- \(a^3+b^3=(a+b)(a^2-ab+b^2)\)
- \(a^3-b^3=(a-b)(a^2+ab+b^2)\)
- \(a^3+b^3+c^3-3abc=(a+b+c)(a^2+b^2+c^2-ab-bc-ca)\)

公式はちゃんと正しく覚えて使いこなそう!
手順3:最低次数の文字に注目【例題①】

共通因数はない。
公式も使えない。
だから手順3を考える!
最低次数の文字について降べきの順に並べる
\(x^3+x^2y-x^2-y\) において、
\(x\) , \(y\) のそれぞれの次数に注目すると、
\(x\)・・・3 次式
\(y\)・・・1 次式
つまり、次数の低い \(y\) に注目して、降べきの順に並べる
\(x^3+x^2y-x^2-y=(x^2-1)y+(x^3-x^2)\)
それぞれで因数分解
\(x^3+x^2y-x^2-y=(x^2-1)y+(x^3-x^2)\) において、
・\((x^2-1)y=(x+1)(x-1)y\)
・\((x^3-x^2)=x^2(x-1)\) より
\(x^3+x^2y-x^2-y\\=(x^2-1)y+(x^3-x^2)\\=(x+1)(x-1)y+x^2(x-1)\)
共通因数でくくる or 式全体でたすきがけ
\(x^3+x^2y-x^2-y=(x+1)(x-1)y+x^2(x-1)\) において、
\(x-1\) の共通因数を持つため、
\(x^3+x^2y-x^2-y\\=(x^2-1)y+(x^3-x^2)\\=(x+1)(x-1)y+x^2(x-1)\\=(x-1)\left\{(x+1)y+x^2\right\}\\=(x-1)(x^2+xy+y)\)
手順3:最低次数の文字に注目【例題②】
最低次数の文字について降べきの順に並べる
\(2x^2+5xy+3y^2-3x-5y-2\) において、
\(x\) , \(y\) のそれぞれの次数に注目すると、
\(x\)・・・2 次式
\(y\)・・・2 次式
次数が同じときはどちらでもよい
今回は、\(x\) に注目して、降べきの順に並べる
\(2x^2+5xy+3y^2-3x-5y-2\\=2x^2+(5y-3)x+(3y^2-5y-2)\)
それぞれで因数分解
\(2x^2+5xy+3y^2-3x-5y-2=2x^2+(5y-3)x+(3y^2-5y-2)\) において、
・\(2x^2\) 、\((5y-3)x\) はこれ以上因数分解できないためそのまま
・\(3y^2-5y-2=(y-2)(3y+1)\) より
\(2x^2+5xy+3y^2-3x-5y-2=2x^2+(5y-3)x+(y-2)(3y+1)\)
共通因数でくくる or 式全体でたすきがけ
\(2x^2+5xy+3y^2-3x-5y-2=2x^2+(5y-3)x+(y-2)(3y+1)\) において、
共通因数はないため、式全体でたすきがけを行う.
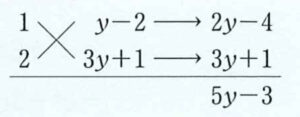
したがって、
\(2x^2+5xy+3y^2-3x-5y-2=(x+y-2)(2x+3y+1)\)
まとめ
因数分解は完全パターンです。
大きな手順としては
- 共通因数でくくる
- 公式の利用
- 最低次数の文字に注目
→ 降べきの順
→ それぞれで因数分解
→ 共通因数でくくる or 式全体でたすきがけ
の流れを覚えた上で、しっかりと演習を行いましょう!







コメント