【2021京都大学・理系・第４問】
曲線 \(y=\log(1+\cos x)\) の \(0≦x≦\displaystyle\frac{\pi}{2}\) の部分の長さを求めよ．
曲線の長さについて
京都大学では、2009年、2002年にも曲線の長さが出題されています。
定期的に出題される問題になりますので、しっかりと確認をしておきましょう！
媒介変数された曲線の長さ
曲線 \(x=f(t)\) , \(y=g(t)\) ( \(\alpha≦t≦\beta\) ) の長さ \(L\) は
\(L=\displaystyle\int^{\beta}_{\alpha}\sqrt{\left(\displaystyle\frac{dx}{dt}\right)^2+\left(\displaystyle\frac{dy}{dt}\right)^2} dt=\displaystyle\int^{\beta}_{\alpha}\sqrt{\left\{f^{\prime}(t)\right\}^2+\left\{g^{\prime}(t)\right\}^2} dt\)
曲線の方程式が媒介変数 \(t\) を用いて \(x=f(t)\) , \(y=g(t)\) ( \(\alpha≦t≦\beta\) ) と表され，\(f(t)\) , \(g(t)\) の導関数はともに連続であるとき，この曲線の長さ \(L\) について
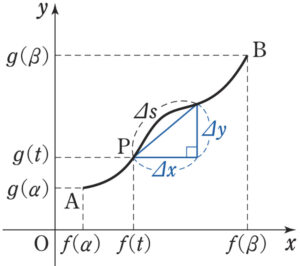\(A (f(\alpha) , g(\alpha))\) ，\(B (f(\beta) , g(\beta))\) とする．
点 \(A\) から \(P (f(t) , g(t))\) までの曲線の長さを \(t\) の関数として考え，\(s(t)\) と表す．
また，\(t\) の増分 \(Δt\) に対する \(s(t)\) , \(f(t)\) , \(g(t)\) の増分をそれぞれ \(Δs\) , \(Δx\) , \(Δy\) とし， \(|Δt|\) が十分に小さいとき
\(|Δs| ≒ \sqrt{\left(Δx\right)^2+\left(Δy\right)^2}\) ・・・① と考えられる．
①より，\(\displaystyle\frac{Δs}{Δt} ≒ \sqrt{\left(\displaystyle\frac{Δx}{Δt}\right)^2+\left(\displaystyle\frac{Δy}{Δt}\right)^2}\) ・・・②
\(Δt \rightarrow 0\) のとき②より
\(\displaystyle\frac{ds}{dt}=\sqrt{\left\{f^{\prime}(t)\right\}^2+\left\{g^{\prime}(t)\right\}^2}\)
よって，\(s(t)\) は \(t\) の関数 \(\sqrt{\left\{f^{\prime}(t)\right\}^2+\left\{g^{\prime}(t)\right\}^2}\) の不定積分の \(1\) つであるから
\(\displaystyle\int^{\beta}_{\alpha}\sqrt{\left\{f^{\prime}(t)\right\}^2+\left\{g^{\prime}(t)\right\}^2} dt=s(\beta)-s(\alpha)\)
ここで，\(s(\alpha)=0\) , \(s(\beta)=L\) であるから
\(L=\displaystyle\int^{\beta}_{\alpha}\sqrt{\left\{f^{\prime}(t)\right\}^2+\left\{g^{\prime}(t)\right\}^2} dt\)
曲線 \(y=f(x)\) の長さ
曲線 \(y=f(x)\) ( \(a≦x≦b\) ) の長さ \(L\) は
\(L=\displaystyle\int^{b}_{a}\sqrt{1+\left(\displaystyle\frac{dy}{dx}\right)^2} dx=\displaystyle\int^{b}_{a}\sqrt{1+\left\{f^{\prime}(x)\right\}^2} dx\)
曲線 \(x=t\) , \(y=g(t)\) と考えると，
\(\displaystyle\frac{dx}{dt}=1\) , \(\displaystyle\frac{dy}{dt}=\displaystyle\frac{dy}{dx}\cdot\displaystyle\frac{dx}{dt}=\displaystyle\frac{dy}{dx}=f^{\prime}(x)\)
となるので，上で求めた
\(L=\displaystyle\int^{\beta}_{\alpha}\sqrt{\left(\displaystyle\frac{dx}{dt}\right)^2+\left(\displaystyle\frac{dy}{dt}\right)^2} dt=\displaystyle\int^{\beta}_{\alpha}\sqrt{\left\{f^{\prime}(t)\right\}^2+\left\{g^{\prime}(t)\right\}^2} dt\)
に代入すると得られる．
2021京大：解答・解説
【2021京都大学・理系・第４問】
曲線 \(y=\log(1+\cos x)\) の \(0≦x≦\displaystyle\frac{\pi}{2}\) の部分の長さを求めよ．
求める曲線の長さを \(L\) とする．
\(y=\log(1+\cos x)\) について，
\(y^{\prime}=\displaystyle\frac{-\sin x}{1+\cos x}\) より
\(1+\left(y^{\prime}\right)^2=1+\displaystyle\frac{\sin^2x}{(1+\cos x)^2}\)
\(=\displaystyle\frac{2+2\cos x}{(1+\cos x)^2}=\displaystyle\frac{2}{1+\cos x}\)
ここで半角の公式から，\(\cos^2\displaystyle\frac{x}{2}=\displaystyle\frac{1+\cos x}{2}\) より
\(1+\left(y^{\prime}\right)^2=\displaystyle\frac{1}{\cos^2\displaystyle\frac{x}{2}}\) であるから
\(0≦x≦\displaystyle\frac{\pi}{2}\) において \(\cos \displaystyle\frac{x}{2}>0\) であるから
\(L=\displaystyle\int^{\frac{\pi}{2}}_{0}\sqrt{1+\left(y^{\prime}\right)^2} dx=\displaystyle\int^{\frac{\pi}{2}}_{0}\displaystyle\frac{1}{\cos\frac{x}{2}} dx\)
\(t=\displaystyle\frac{x}{2}\) とおくと
\(L=2\displaystyle\int^{\frac{\pi}{4}}_{0}\displaystyle\frac{1}{\cos t} dt\)
分母分子に \(\cos t\) をかけると
\(L=2\displaystyle\int^{\frac{\pi}{4}}_{0}\displaystyle\frac{\cos t}{\cos^2 t} dt=2\displaystyle\int^{\displaystyle\frac{\pi}{4}}_{0}\displaystyle\frac{\cos t}{1-\sin^2 t} dt\)
\(u=\sin t\) とおくと
\(L=2\displaystyle\int^{\frac{1}{\sqrt{2}}}_{0}\displaystyle\frac{1}{1-u^2} du\)
\(=2\displaystyle\int^{\frac{1}{\sqrt{2}}}_{0}\displaystyle\frac{1}{2}\left(\displaystyle\frac{1}{1-u}+\displaystyle\frac{1}{1+u}\right)du\)
\(=\Bigl[-\log(1-u)+\log(1+u)\Bigr]^{\frac{1}{\sqrt{2}}}_{0}\)
\(=2\log(\sqrt{2}+1)\)
コメント