【2023早稲田大学・商学部・第１問(３)】
\(n\) を正の整数とする．次の条件( ⅰ )，( ⅱ )，( ⅲ )を満たす \(n\) 次関数 \(f(x)\) のうち \(n\) が最小のものは，\(f(x)=\) [ ウ ] である．
( ⅰ ) \(f(1)=2\)
( ⅱ ) \(\displaystyle\int^{1}_{-1}(x+1)f(x) dx=0\)
( ⅲ ) すべての正の整数 \(m\) に対して，\(\displaystyle\int^{1}_{-1}|x|^mf(x) dx=0\)
偶関数・奇関数の定積分について
\(f(x)\) が偶関数のとき
\(\displaystyle\int^{a}_{-a}f(x) dx=2\displaystyle\int^{a}_{0}f(x) dx\)
\(f(x)\) が奇関数のとき
\(\displaystyle\int^{a}_{-a}f(x) dx=0\)
積分区間が異符号(\(-a\)，\(a\))の値の定積分を考えるとき，
偶関数・奇関数の性質が利用できないか考える癖を！
偶関数とは
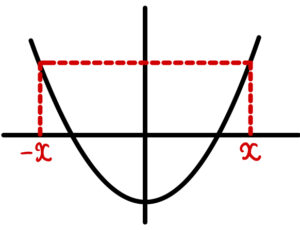\(y\) 軸に関して対称なグラフ：\(f(x) = f(-x)\)
例：\(y=3\) (定数関数)、\(y=x^2\)、\(y=\cos x\) など
奇関数とは
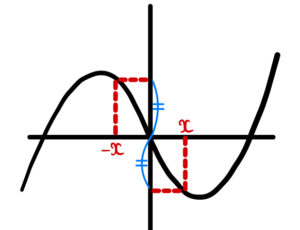原点に関して対称なグラフ：\(f(-x) = -f(x)\)
例：\(y=x\)、\(y=x^3\)、\(y=\sin x\)、\(y=\tan x\) など
条件( ⅲ )の \(|x|^m\) は偶関数！
つまり、\(\displaystyle\int^{1}_{-1}|x|^mf(x) dx=0\) を満たすとき
\(|x|^mf(x)\) は奇関数でなければいけないので，\(f(x)\) は奇関数であると分かりますね！
解答・解説
\(g(x)=|x|^m\) とおくと
\(g(-x)=|-x|^m=|x|^m=g(x)\) より，\(|x|^m\) は偶関数である．
条件( ⅲ )からすべての整数 \(m\) に対して
\(\displaystyle\int^{1}_{-1}|x|^mf(x) dx=0\)
が成立するとき，\(|x|^mf(x)\) は奇関数となるため，
\(f(x)\) は奇関数となる．
よって，\(n=1,3,5,\cdots\) を順に考えればよい．
( ア ) \(n=1\) のとき
\(f(x)=ax\) ( \(a\not=0\) ) とおくことができる
条件( ⅰ ) \(f(1)=2\) より \(a=2\)
よって \(f(x)=2x\)
このとき
\(\displaystyle\int^{1}_{-1}(x+1)\cdot 2x dx=\displaystyle\int^{1}_{-1}(2x^2+2x) dx\not=0\) より
条件( ⅱ )を満たさないため不適．
( イ ) \(n=3\) のとき
\(f(x)=ax^3+bx\) ( \(a\not=0\) ) とおくことができる
条件( ⅰ ) \(f(1)=2\) より \(a+b=2\) \(\iff\) \(b=2-a\)
よって \(f(x)=ax^3+(2-a)x\)
このとき
\(\displaystyle\int^{1}_{-1}(x+1)\cdot \left\{ax^3+(2-a)x\right\} dx\)
\(=\displaystyle\int^{1}_{-1}\left\{ax^4+ax^3-(a-2)x^2-(a-2)x\right\} dx\)
\(=2\displaystyle\int^{1}_{0} \left\{ax^4-(a-2)x^2\right\}dx\)
\(=2\Bigl[\displaystyle\frac{a}{5}x^5-\displaystyle\frac{a-2}{3}x^3\Bigr]^{1}_{0}\)
\(=\displaystyle\frac{2a}{5}-\displaystyle\frac{2(a-2)}{3}\)
\(=\displaystyle\frac{-4a+20}{15}\)
条件( ⅲ )を満たす実数 \(a\) は
\(\displaystyle\frac{-4a+20}{15}=0\) \(\iff\) \(a=5\)
ゆえに，\(f(x)=5x^3-3x\) は適する．
したがって，求める関数は \(f(x)=5x^3-3x\)
コメント