【2022大阪医科薬科大学・看護・[2]】

解答・解説
(1) \(k=4\) のとき、方程式①の解
\(x^2-kx-\displaystyle\frac{k}{2}+2=0\) ・・・①
\(k=4\) のとき ① は,
\(x^2-4x=0\) \(\iff\) \(x(x-4)=0\)
よって,\(x=0\) または \(4\) ・・・( c )
(2) 方程式①が \(x=2\) を解にもつ
\(x=2\) を ① に代入すると,
\(4-2k-\displaystyle\frac{k}{2}+2=0\)
よって,\(k=\displaystyle\frac{12}{5}\) ・・・(e)
(3) 方程式①が実数解をもつ条件
①の判別式を \(D\) とすると,\(D≧0\) となればよいので,
\(D=(-k)^2-4\cdot 1 \cdot \left(-\displaystyle\frac{k}{2}+2\right)≧0\)
\(k^2+2k-8≧0\)
\((k+4)(k-2)≧0\)
\(k≦-4\) または \(2≦k\) ・・・( b )
(4) \(0≦x≦2\) に①が \(1\) つだけ実数解をもつ
( ⅰ ) \(0<x<2\) と \(x<0,2<x\) にそれぞれ \(1\) つずつ解をもつとき
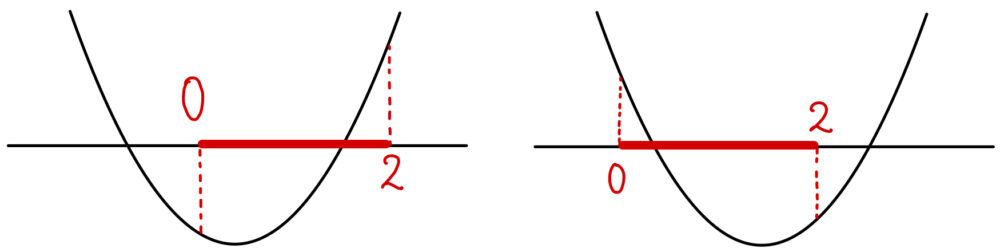
『 \(f(0)<0\) かつ \(f(2)>0\) 』または『 \(f(0)>0\) かつ \(f(2)<0\) 』
\(\iff\) \(f(0)\times f(2)<0\)
よって,\(\left(-\displaystyle\frac{k}{2}+2\right)\left(-\displaystyle\frac{5k}{2}+6\right)<0\)
\((k-4)(5k-12)<0\)
よって,\(\displaystyle\frac{12}{5}<k<4\)
( ⅱ ) \(x=0\) を解に持つとき
\(f(0)=0\) \(\iff\) \(-\displaystyle\frac{k}{2}+2=0\)
よって,\(k=4\)
このとき (1) より,①の解は \(x=0,4\) となり題意を示す.
( ⅲ ) \(x=2\) を解に持つとき
(2) より,\(k=\displaystyle\frac{12}{5}\)
このとき ①は
\(x^2-\displaystyle\frac{12}{5}x+\displaystyle\frac{4}{5}=0\)
\((x-2)\left(x-\displaystyle\frac{2}{5}\right)=0\)
\(x=2,\displaystyle\frac{2}{5}\)
これは題意を示さない.
( ⅰ )〜( ⅲ )より,\(\displaystyle\frac{12}{5}<k≦4\) ・・・( e )
(5) \(0≦x≦2\) に①が少なくとも \(1\) つの実数解
\(0≦x≦2\) に \(2\) つ(重解を含む)をもつとき
(ア) \(D≧0\)
(イ) \(0≦軸≦2\)
(ウ) \(f(0)≧0,f(2)≧0\)
を満たせばよい.
(ア) \(D≧0\) について
(3)より,\(k≦-4\) または \(2≦k\)
(イ) \(0≦軸≦2\) について
\(x^2-kx-\displaystyle\frac{k}{2}+2=\left(x-\displaystyle\frac{k}{2}\right)^2-\displaystyle\frac{k^2}{4}-\displaystyle\frac{k}{2}+2\) より
\(0≦\displaystyle\frac{k}{2}≦2\) \(\iff\) \(0≦k≦4\)
(ウ) \(f(0)≧0,f(2)≧0\) について
\(f(0)=-\displaystyle\frac{k}{2}+2≧0\)
よって,\(k≦4\)
\(f(2)=-\displaystyle\frac{5k}{2}+6≧0\)
よって,\(k≦\displaystyle\frac{12}{5}\)
(ア)〜(ウ)より,\(2≦k≦\displaystyle\frac{12}{5}\) ・・・②
また(4)より,\(0≦x≦2\) に \(1\) つ(重解を除く)をもつとき
\(\displaystyle\frac{12}{5}<k≦4\) ・・・③
②,③より \(2≦k≦4\) ・・・( d )








コメント