【2014中央大学(一部)】
座標平面上で,点 \((x,y)\) を考える.ここで,\(x\) , \(y\) を \(0\) 以上の整数,\(n\) を自然数とする.
このとき,以下の個数を \(n\) で表せ.
(1) \(x+y≦n\) を満たす点 \((x,y)\) の個数
(2) \(\displaystyle\frac{x}{2}+y≦n\) を満たす点 \((x,y)\) の個数
格子点について
格子点とは
格子点とは,\(x\) 座標も \(y\) 座標も整数である点のこと.

難関大学では頻出の分野の1つです!
有名な問題ですので,しっかりと考え方をマスターしましょう!
格子点問題の考え方
格子点
⇒ \(x\) or \(y\) 軸に平行な直線ごとにカウントし,総和(Σ)を考える
(1) 解答・解説
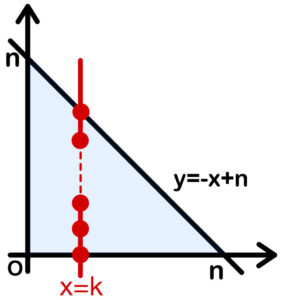
\(x≧0\) , \(y≧0\) , \(x+y≦n\) を満たす領域の中で
\(x=k\) ( \(k=0,1,2,\cdots,n\) ) 上にある格子点は
\((k,0)\) , \((k,1)\) , \((k,2)\) , ・・・ , \((k,-k+n)\) の
\(-k+n+1\) 個ある.
したがって,
\(\displaystyle\sum_{k=0}^{n}{(-k+n+1)}=n+1+\displaystyle\sum_{k=1}^{n}{(-k+n+1)}\)
\(=n+1-\displaystyle\frac{1}{2}n(n+1)+n(n+1)\)
\(=\displaystyle\frac{1}{2}(n+1)(n+2)\) 個
(2) 解答・解説
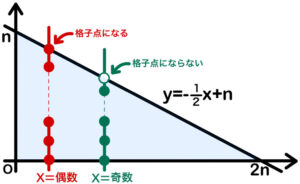

上図のように(1)と同様に \(x=k\) で考えると,
\(x\) が偶数の場合と奇数の場合で,\(y=-\displaystyle\frac{1}{2}x+n\) 上の点が格子点になるかどうかが変わります。つまり場合分けをしなければいけません!
そんな時は, \(y=k\) を考えてみましょう!
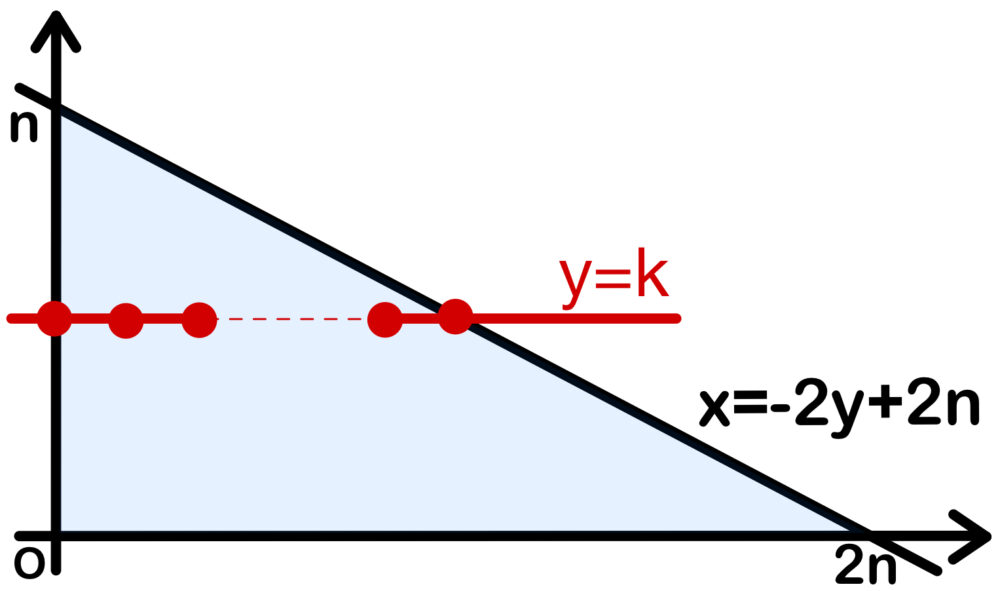
\(x≧0\) , \(y≧0\) , \(x+y≦n\) を満たす領域の中で
\(y=k\) ( \(k=0,1,2,\cdots,n\) ) 上にある格子点は
\((0,k)\) , \((1,k)\) , \((2,k)\) , ・・・ , \((-2k+2n,k)\) の
\(-2k+2n+1\) 個ある.
したがって,
\(\displaystyle\sum_{k=0}^{n}{(-2k+2n+1)}=2n+1+\displaystyle\sum_{k=1}^{n}{(-2k+2n+1)}\)
\(=2n+1-\displaystyle\frac{2}{2}n(n+1)+n(2n+1)\)
\(=(n+1)^2\) 個









コメント